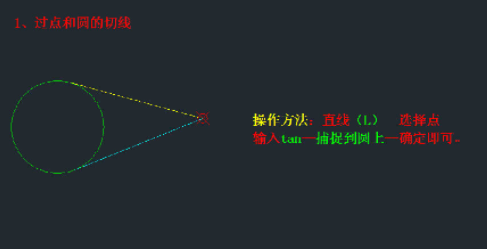
如果函数在某点不可导，该点的切线存在吗

存在，存在斜率是可导的必要不充分条件。可导必须要存在极限。

几何上，切缏堋垌胯线指的是一条刚好触碰到曲线上某一点的直线。更准确地说，当切线经过曲线上的某点（即切点）时，切线的方向与曲线上该点的方向是相同的。平面几何中，将和圆只有一个公共交点的直线叫做圆的切线。

在高等数学中，对于一个函数，如果函数某处有导数，那么此处的导数就是过此处的切线的斜率，该点和斜率所构成的直线就为该函数的一个切线。

性质定理：

圆的切线垂直于过其切点的半径；经过半径的非圆心一端，并且垂直于这条半径的直线，就是这个圆的一条切线。

判定定理

一直线若与一圆有交点，且连接交点与圆心的直线与该直线垂直，那么这条直线就是圆的切线。

一般可用：

1、作垂直证半径

2、作半径证垂直