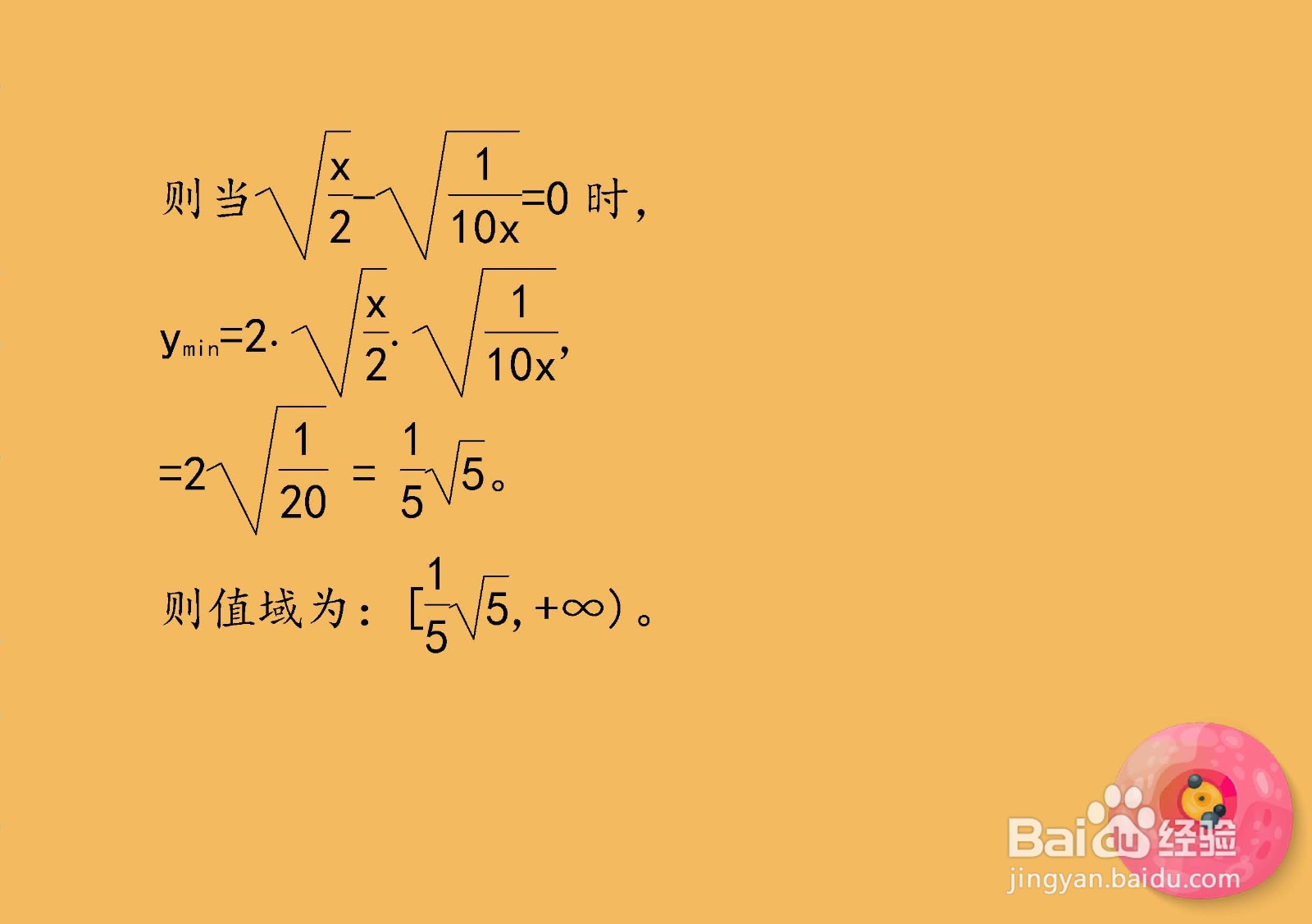分数复合函数y=x/2+1/10x的值域

1、 通过基本不等式法、配方法、导数法等，介绍求函数y=x/2+1/10x在x>0时值域的主要过程与步骤。

2、主要思路：将函数y=x/2+1/10x变形为x的二次函数，再利用二次方程判别式计算求解函数的值域。∵y租涫疼迟=1x/2+1/10x∴20xy=10x^2+2，即：10x^2-20xy+2=0,化简变形得：5x^2-10y*x+1=0,方程对x有解，则：

3、判别式△=猾诮沓靥(10y)^2-4*5≥0，解得：y^2≥4*5/10^2,所以：y≥2/10*√5=(1/5)*√5.则y=x/2+1/10x值域为：[(1/5)*√5,+∞)。

4、y=1x/2+1/10x≥2√(1x/2*1/10x),=2√(1/20)=(1/5)*√5.则值域为：[(1/5)*√5,+∞)。

5、y=1x/2+1/10x=[√(1x/2)]^2+[俑啪压锑√(1/10x)]^2=[√(1x/2)-√(1/10x)]^2+2√(1x/2)*√(1/10x)则当√(1x/2)-√(1/10x)=0时，ymin=2√(1x/2)*√(1/10x)=2√(1/20)=(1/5)*√5。则值域为：[(1/5)*√5,+∞)。

6、将所求函数y=x/2+1/10x配方成为含有x的二次方程，再根据二次函数的性质求解值域。

7、用导数求出函数y=x/2+1/10x的驻点，在判断函数的单调性，进而求出函数的最值，最终得到函数y=x/2+1/10x的值域。