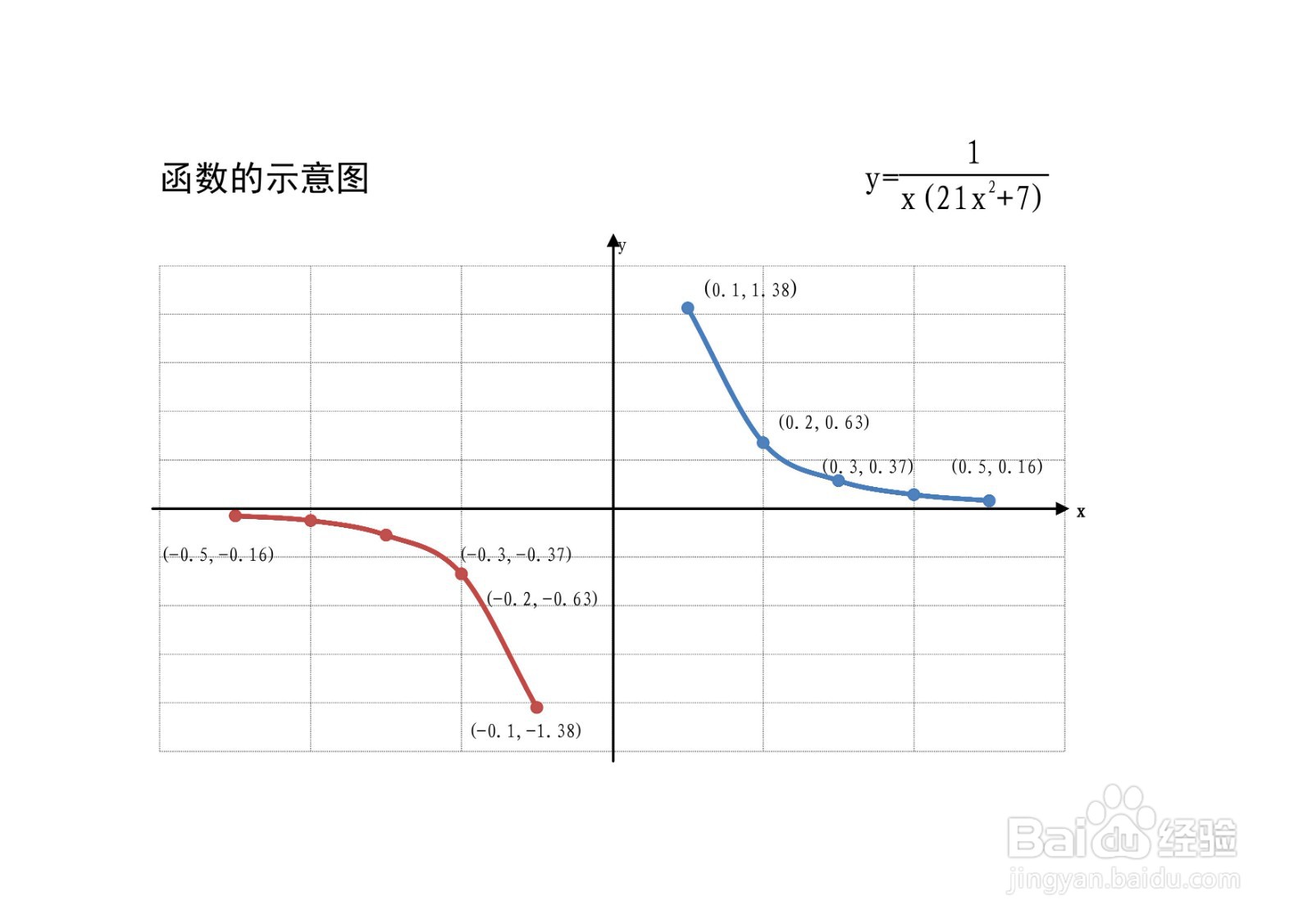
如何画函数y=1/x(21x^2+7)的图像示意图

1、由分数函数的定义域、值域、单调性、凸凹性、极限等主要函数性质，并通过导数知识求解计算函数的单调区间和凸凹区间，同时综合函数性质画出该函数图像的示意图。

2、函数的定义域和值域解析过程。

3、函数的单调性，计算函数的一阶导数，解析函数的单调性，求出函数的单调区间。

4、 函数的单调性是函数的重要性质，反映了随着自变量的增加函数值的变化趋势，它是研究函数性质的有力工具，在解决比较大小、解决函数图像、值域、最值、不等式问题都有很重要的作用。

5、如果函数f(x)在区间I上二阶可导，则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。

6、设函数f(x),|x|大于某一一冶嚏型正数时有定义，若存在常数A，对于任意ε>0，总存在正整数X，使得当x>X时，|f(x)-A|<ε成立，那么称A是函数f(x)在无穷大处的极限。

7、在数学中，一个函数f(x) 被称为奇函数，当且仅当对于任意实数x，都有f(-x)=颍骈城茇-f(x)成立；而一个函数f(x)f(x)被称为偶函数，当且仅当对于任意实数 x，都有f(-x)=f(x) 成立。判断一个函数的奇偶性可以通过代入-x并进行比较的方法进行。具体来说：对于奇函数f(x)，我们有f(-x)=-f(x)，因此f(-x)+f(x)=0。对于偶函数f(x)，我们有f(-x)=f(x)，因此f(-x)-f(x)=0。

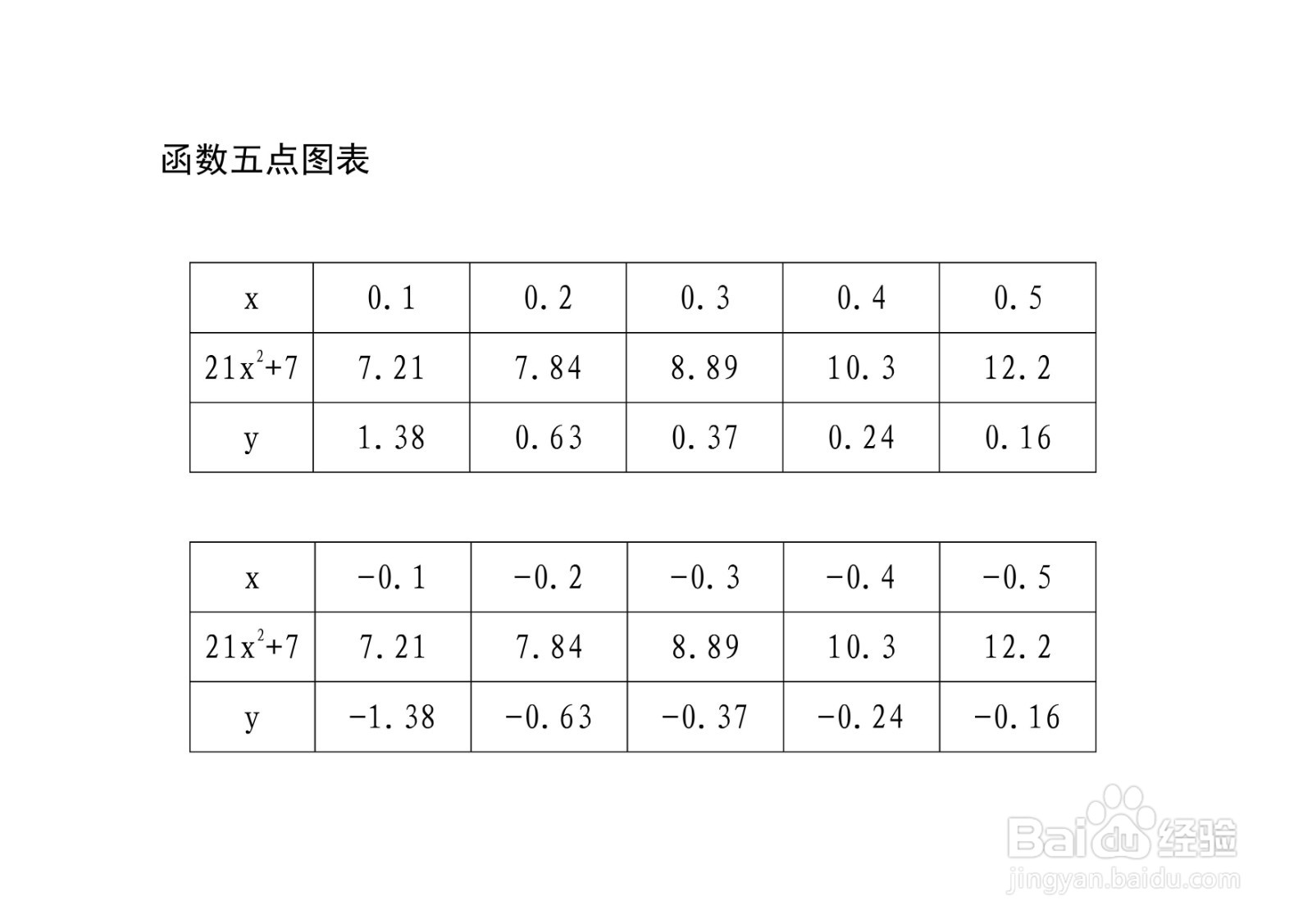
8、函数五点图解析表如下：

9、根据以上函数的定义、单调、凸凹等性质，结合函数的单调和凸凹区间及极限等性质，函数的示意图可以简要画出。