直观了解反函数的相关知识

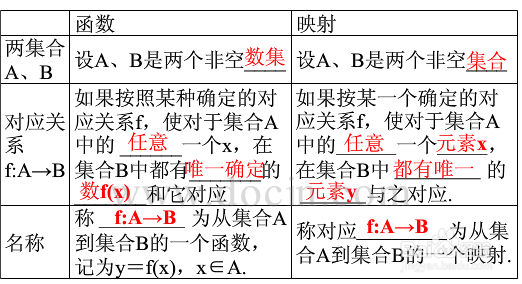
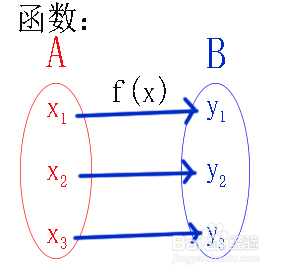
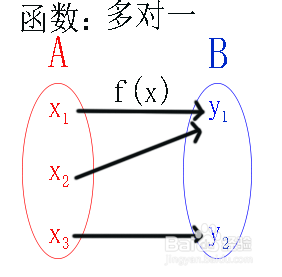
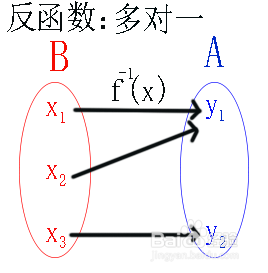
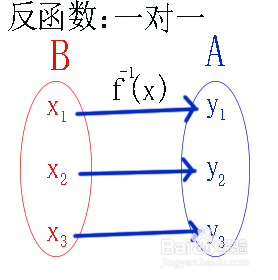
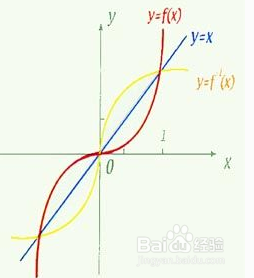
1、反函数的定义：设函数y=f(x)的定义域是D，值域是f(D)。如果对于值域f(D)中的每一个鲻戟缒男y，在D中有且只有一个x使得f(x)=y，则按此对应法则脲摩喜清得到了一个定义在f(D)上的函数，并把该函数称为函数y=f(x)的反函数。为了更好的理解反函数的定义，我们首先来分析一下函数和反函数的关系。

2、接下来我们就要在函数的基础上了解反函数的定义。确定反函数中所需要的必要条件。

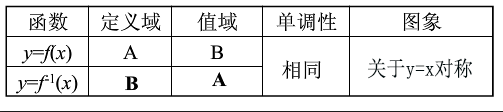
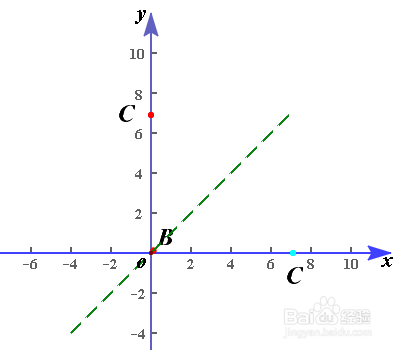
3、我们分析一下反函数的定义域与值域的关系，看有没有什么发现？是不是能找到反函数中的相关条件。

4、大部分偶函数不存在反函数（当函数y=f(x)， 定义域是{0} 且 f(x)=C （其中C是常数），则函数f(x)是偶函数且有反函数，其反函数的定义域是{C}, 值域为{0} ）。奇函数不一定存在反函数，被与y轴垂直的直线截时能过2个及以上点即没有反函数。若一个奇函数存在反函数，则它的反函数也是奇函数。

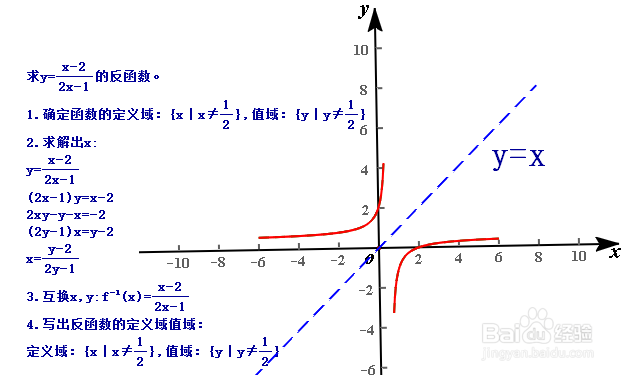
5、反函数的定义，和相关性质在题目中的应用。求函数y=f(x)的反函数的一般步骤是：①确定函数y=f(x)的定义域和值域；②视y=f(x)为关于x的方程，解方程得x=f-1(y);③互换x,y得反函数的解析式y=f-1(x)；④写出反函数的定义域（原函数的值域）。

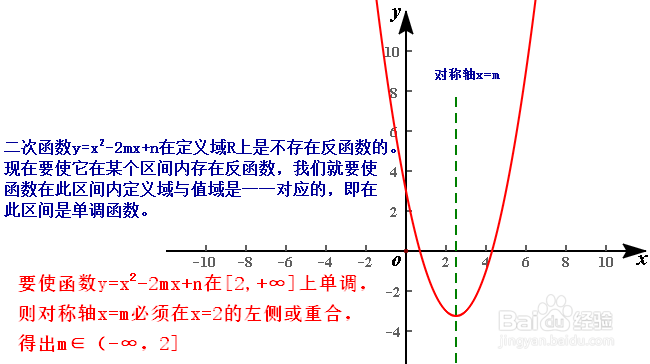
6、为了更深入的了解反函数，我们再看一个关于反函数的变式问题:若函数f(x)=x²-2mx+n在区间[2,+∞)上存在反函数，则m的取值范围是 多少？

7、关于这个知识，我们要了解函数什么时候存在反函数，了解反函数的意义及其相关性质对我们解题有很大的帮助，也要适应数学题中的一些变式，会分析题目。对我们学好数学非常重要。