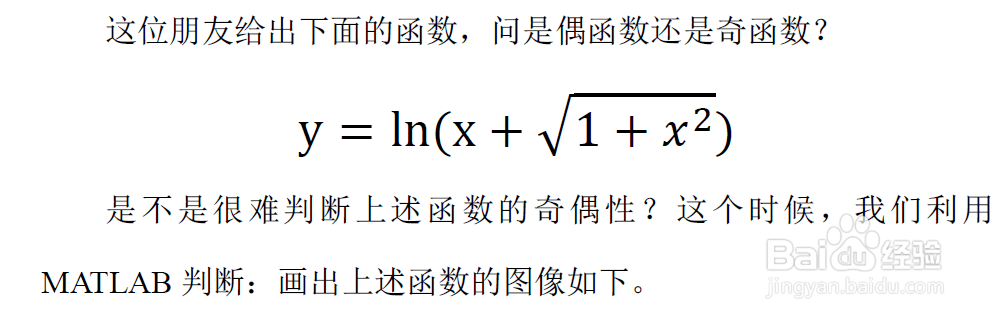MATLAB判断函数y=ln(x+sqrt(1+x^2))的奇偶性

1、第一，判断下图函数的奇偶性，该函数奇偶性很难判断，所以利用MATLAB来判断。

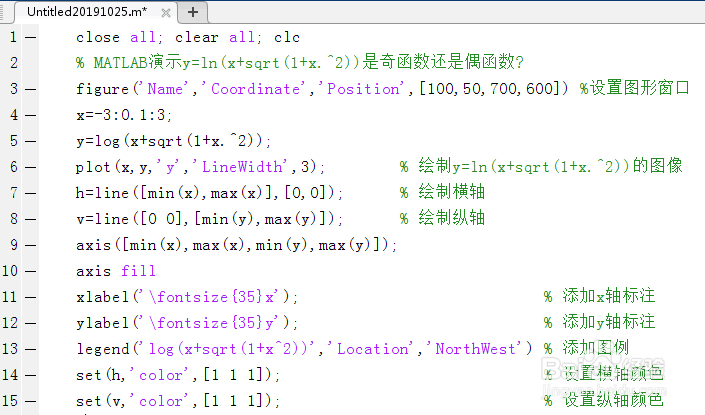
2、第二，启动MATLAB，输入如下代码。close all; clear all; clc% MATLAB演示y=ln(x+sqrt(1+x.^2))是奇函数还是偶挣窝酵聒函数?figure('Name','Coordinate','Position',[100,50,700,600]) %设置图形窗口x=-3:0.1:3; y=log(x+sqrt(1+x.^2)); plot(x,y,'y','LineWidth',3); % 绘制y=ln(x+sqrt(1+x.^2))的图像h=line([min(x),max(x)],[0,0]); % 绘制横轴v=line([0 0],[min(y),max(y)]); % 绘制纵轴axis([min(x),max(x),min(y),max(y)]);axis fillxlabel('\fontsize{35}x'); % 添加x轴标注ylabel('\fontsize{35}y'); % 添加y轴标注legend('log(x+sqrt(1+x^2))','Location','NorthWest') % 添加图例set(h,'color',[1 1 1]); % 设置横轴颜色set(v,'color',[1 1 1]); % 设置纵轴颜色

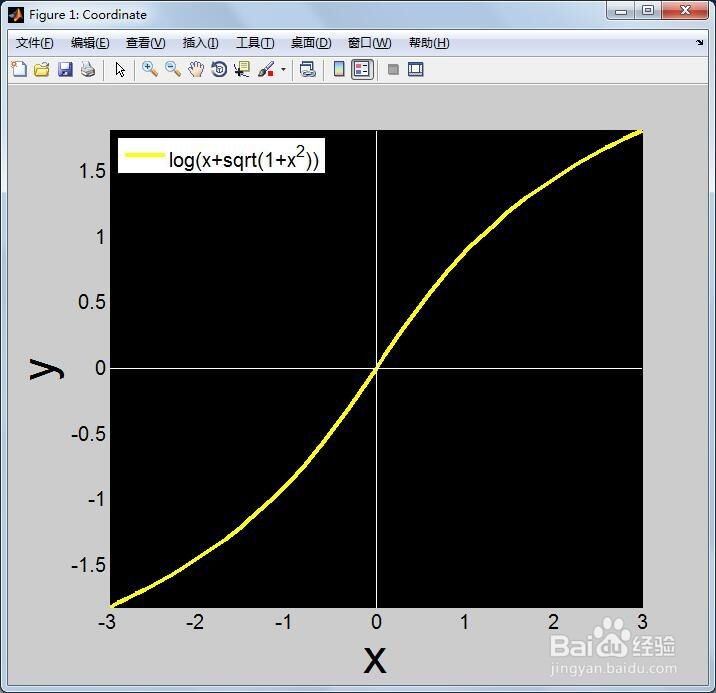
3、第三，保存和运行上述代码，得到函数y=ln(x+sqrt(1+x^2))的图像如下。在MATLAB中log表示ln的意思。

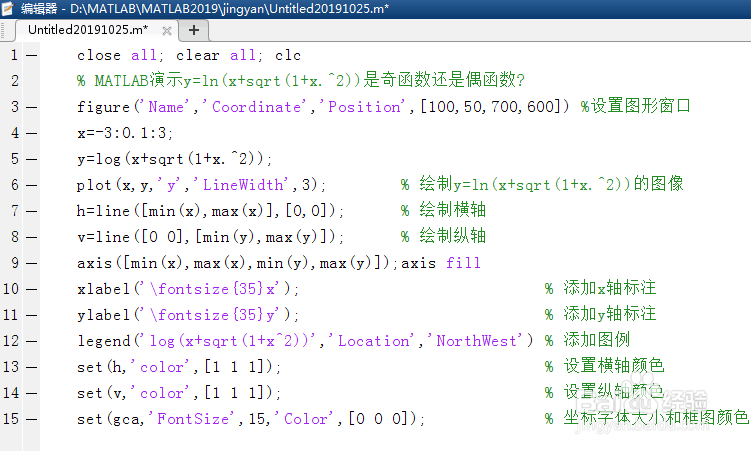
4、第四，在上述代码末尾添加set(gca,'FontSize',15,'Color',[0 0 0])，改变坐标字体大小和框图颜色。

5、第五，保存和运行上述改进后的代码，得到的函数图像更加美观。

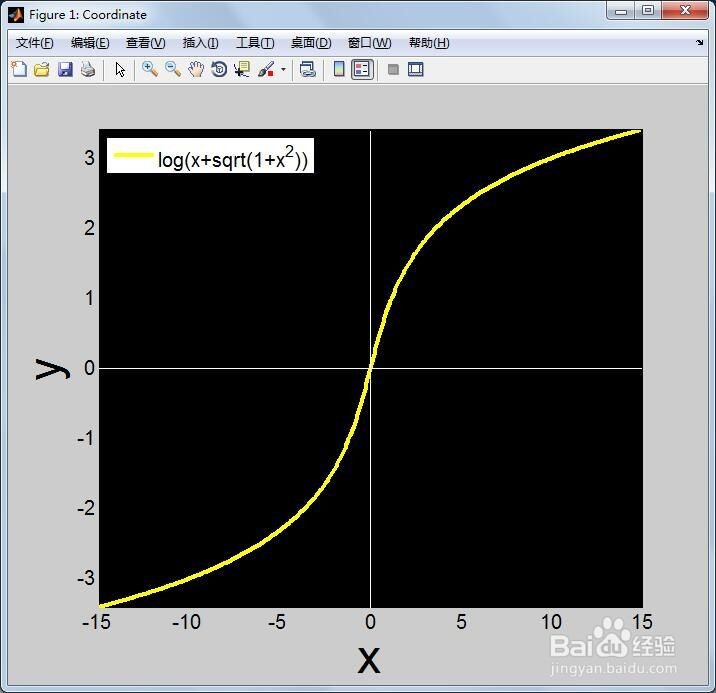
6、第六，可以改变函数的定义域，让值域更宽广，比如使x=-15:0.1:15，再次运行代码脚本，函数的值域更宽广，如下图。