严格凹的效用函数是什么意思

就是一个定义在某个向量空间的凸集C（区间）上的实值函数f。

设f为定义在区间I上的函数，若对I上的任意两点X1<X2和任意的实数λ∈（0，1），总有f(λx1+(1-λ)x2≥λf(x1)+(1-λ)f(x2), 则f称为I上的凹函数。

设函数f(x)在区间I上定义。

若对I中的任意两点x1和x2,和任意λ∈(0,1)，都有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)。

则称f为I上的凸函数(convex function)。若不等号严格成立，即“<”号成立，则称f(x)在I上是严格凸函数。

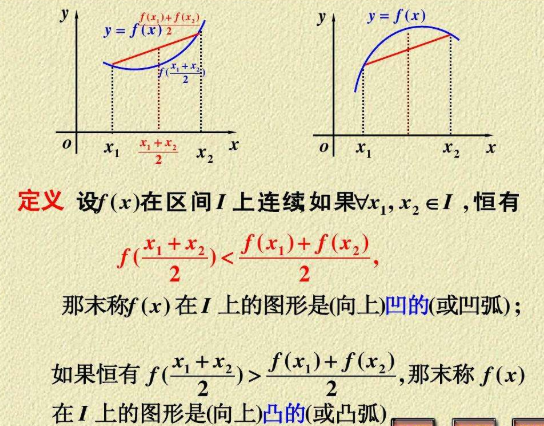
如果"≤“换成“≥”就是凹函数(concave function)。类似也有严格凹函数。设f(x)在区间D上连续，如果对D上任意两点a、b恒有f((a+b)/2)> (f(a)+f(b))/2那么称f(x)在D上的图形是（向下）凸的（或凸弧）。

如果恒有f((a+b)/2)<(f(a)+f(b))/2那么称f(x)在D上的图形是（向下）凹的（或凹弧）。

性质：

如果一个可微函数f它的导数f'在某区间是单调上升的，也就是二阶导数若存在，则在此区间，二阶导数是大于零的，f就是凹的；即一个凹函数拥有一个下跌的斜率，当中下跌只是代表非上升而不是严谨的下跌，也代表这容许零斜率的存在。

如果一个二次可微的函数f，它的二阶导数f'(x)是正值（或者说它有一个正值的加速度），那么它的图像是凹的；如果二阶导数f'(x)是负值，图像就会是凸的。当中如果某点转变了图像的凹凸性，这就是一个拐点。