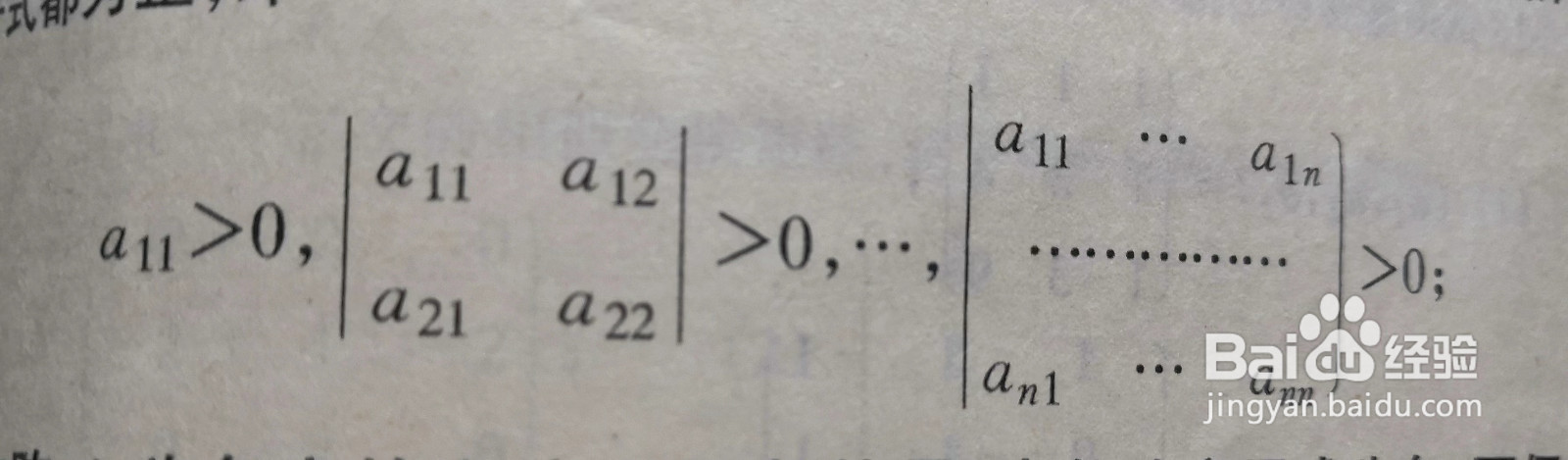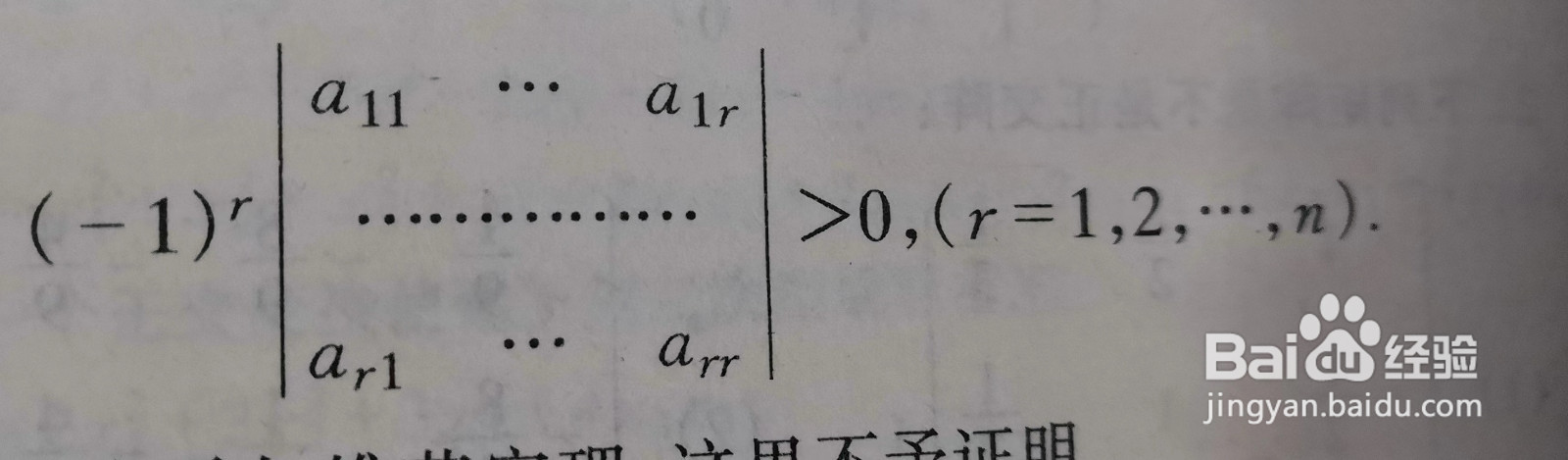怎么判断二次型是否正定

1、设有实二次型f(x)=x'Ax，如果对任何x≠0，都有f(x)>0（显然f(0)=0），则称f为正定二关骇脘骱次型，并称对称阵A是正定的，记作A>0；如果对于任何x≠0都有f(x)<0，则称f为负定二次型，并称对称阵A是负定的，记作A<0。

2、实二次型f(x)=x'Ax为正定的充分必要条件是：它的标准形的n系数全为正。

3、对称阵A为正定的充分必要条件是：A的特征值全为正。

4、对称阵A为正定的充分必要条件是：A的个阶主子式都为正；对称阵A为负定的充分必要条件是：奇数阶主子式为负，偶数阶主子式为正。

5、判别二次型酆璁冻嘌f=-5x²-6y²-4z²+4xy+4xz的正定性。解：f的矩阵为（见图片），根据步骤4可知，该二次型是负定的。