高中数学排列组合21种模型

排列组左佯抵盗合问题也是高中数学中的必考问题，计算相对比较复杂，考题也是非常多变，所以在学习过程中一定要掌握好解题模型，下面我来介绍一下高考中常考的21类模型，希望对大家有帮助。

目录

1、模型一：特殊元素和特殊位置优先策略模型二：相邻元素捆绑策略模型三：不相邻问题插空策略模型四：定序问烙疋艘烯题倍缩空位插入策略模型五：重排问题求幂策略模型六：环排问题线排策略模型七：多排问题直排策略模型八：排列组合混合问题先选后排策略模型九：小集团问题先整体后局部策略模型十：元素相同问题隔板策略模型十一：正难则反总体淘汰策略模型十二：平均分组问题除法策略模型十三：合理分类与分步策略模型十四：构造模型策略模型十六：分解与合成策略模型十七：化归策略模型十八：数字排序问题查字典策略模型十九：树图策略模型二十：复杂分类问题表格策略模型二十一：住店法策略

模型一：特殊元素和特殊位置优先策略

1、例1.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数.

模型二：相邻元素捆绑策略

1、例2. 7人站成一排 ,其中甲乙相邻且丙丁相邻, 共有多少种不同的排法.

模型三：不相邻问题插空策略

1、例3.一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种？

模型四：定序问题倍缩空位插入策略

1、例4. 7人排队,其中甲乙丙3人顺序一定共有多少不同的排法

模型五：重排问题求幂策略

1、例5.把6名实习生分配到7个车间实习,共有多少种不同的分法

模型六：环排问题线排策略

1、例6. 8人围桌而坐,共有多少种坐法?

模型七：多排问题直排策略

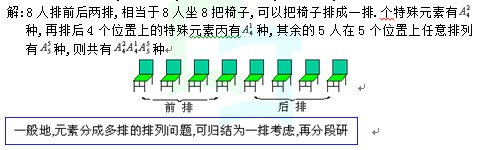
1、例7.8人排成前后两排,每排4人,其中甲乙在前排,丙在后排,共有多少排法

模型八：排列组合混合问题先选后排策略

1、例8. 有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有多少不同的装法.

模型九：小集团问题先整体后局部策略

1、例9. 用1,2,3,4,5组成没有重复数字的五位数其中恰有两个偶数夹1,５在两个奇数之

模型十：元素相同问题隔板策略

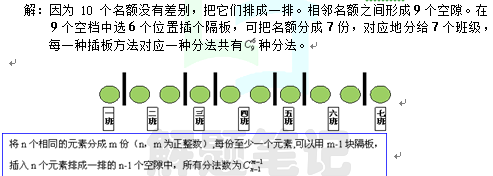
1、例10. 有10个运动员名额，分给7个班，每班至少一个,有多少种分配方案？

模型十一：正难则反总体淘汰策略

1、例11.从0,1,2,3,4,5,6,7,8,9这十个数字中取出三个数，使其和为不小于10的偶数,不同的取法有多少种？

模型十二：平均分组问题除法策略

1、例12. 6本不同的书平均分成3堆,每堆2本共有多少分法？

模型十三：合理分类与分步策略

1、例13. 在一次演唱会上共10名演员,其中8人能能唱歌,5人会跳舞,现要演出一个2人唱歌2人伴舞的节目,有多少选派方法

模型十四：构造模型策略

1、例14. 马路上有编号为1,2,3,4,5,6,7,8,9的九只路灯,现要关掉其中的3盏,但不能关掉相邻的2盏或3盏,也不能关掉两端的2盏,求满足条件的关灯方法有多少种？

模型十五：实际操作穷举策略

1、例15. 设有编号1,2巳呀屋饔,3,4,5的五个球和编号1,2,3,4,5的五个盒子,现将5个球投入这五个盒子内,要求每个盒子放一个球，并且恰好有两个球的编号与盒子的编号相同,有多少投法

模型十六：分解与合成策略

1、例16. 30030能被多少个不同的偶数整除

模型十七：化归策略

1、例17. 25人排成5×5方阵,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种？

模型十八：数字排序问题查字典策略

1、例18．由0，1，2，3，4，5六个数字可以组成多少个没有重复的比324105大的数？

模型十九：树图策略

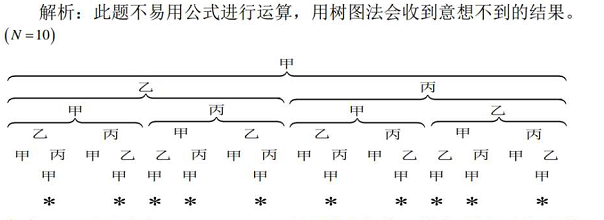
1、例19．人相互传球,由甲开始发球,并作为第一次传球,经过次传求后,球仍回到甲的手中,则不同的传球方式有______

模型二十：复杂分类问题表格策略

1、例20．有红、黄、兰色的球各5只,分别标有A、B、C、D、E五个字母,现从中取5只,要求各字母均有且三色齐备,则共有多少种不同的取法

模型二十一：住店法策略

1、例21.七名学生争夺五项冠军，每项冠军只能由一人获得，获得冠军的可能的种数有多少种？