函数展开成傅里叶级数时所要求的条件是什么

函数展开成傅里叶级数张虢咆噘时所要求的条件是可积；有限间断点；间断点处函数极限存在。

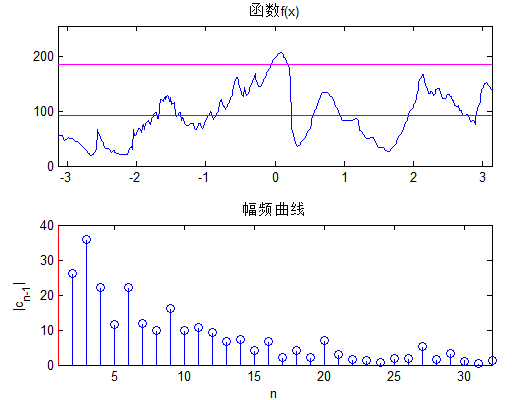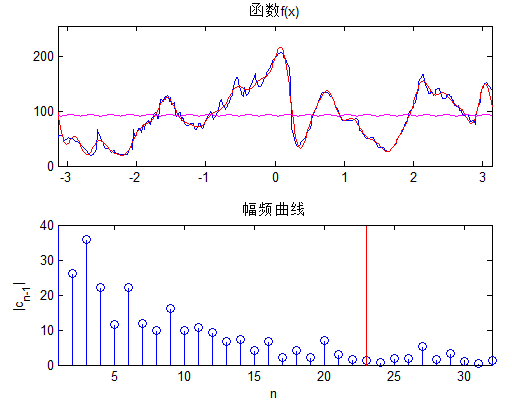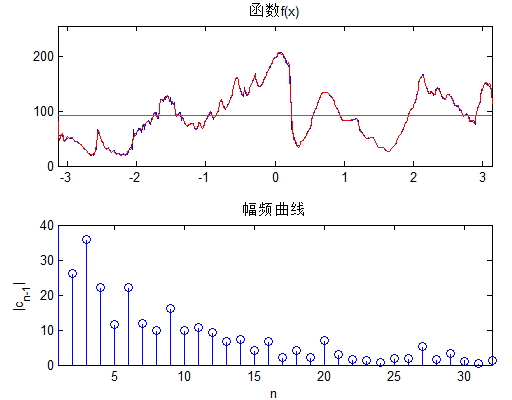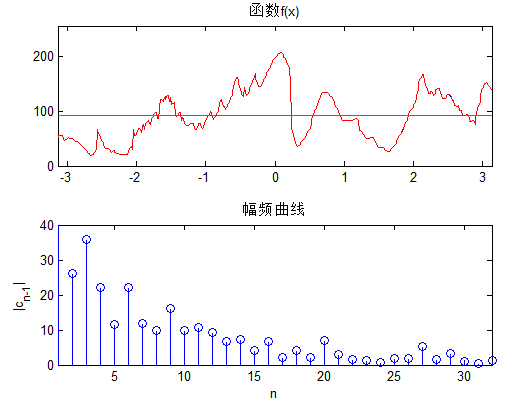
周期为T的函数，故k取不同值时的周期信号具有谐波关系（即它们都具有一个共同周期皈其拄攥T）。k=0时，式中对应的这一项称为直流分量，k=1时具有基波频率。

在任何周期内，x(t)须绝对可积；在任一有限区间中，x(t)只能取有限个最大值或最小值；在任何有限区间上，x(t)只能有有限个第一类间断点。

扩展资料：

两个不同向量正交是指它们的内积为0，这也就意味着这两个向量之间没有任何相关性，例如，在三维欧氏空间中，互相垂直的向量之间是正交的。

事实上，正交是垂直在数学上的的一种抽象化和一般化。一组n个互相正交的向量必然是线性无关的，所以必然可以张成一个n维空间，也就是说，空间中的任何一个向量可以用它们来线性表出。