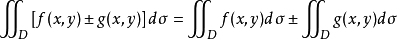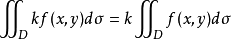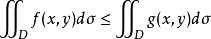为什么两定积分相乘能转化为重积分而且一般上下限相同的的两定积分转化后就能利用对称性求解，我想知道

1、对于一般的二重积分 double integral，仅仅只是一个原则性积分，一般情况下根本是无法积出来的。

2、将二重积器皆阄诟分适当地化为累次积分 iterated integral，积分或许就能迎刃而解；累次积分的顺序不对，可能就积分积不出来；有些积分无论怎样都积不出来的。

3、对于能积分出来的累次积分，其中最最特例是被积函数 integrand如同微分方程一般可以完全分离变量 separable ，而积分区域也是最特殊，各自从一侧积分到另一侧，既如同于矩形区域积分，又如同在圆内用极坐标积分。

这种情况，恰恰就是两个积分的乘积。两个积分的乘积，变成了二重积分，就是这种特例的反演。最典型的例子就是概率统计中的正态函数，也就是误差函数，在从负无穷大到正无穷大的积分，或从0到无穷大的积分。

扩展资料：

积分的线性性质

性质1（积分可加性） 函数和（差）的二重积分等于各函数二重积分的和（差），即

性质2（积分满足数乘） 被积函数的常系数因子可以提到积分号外，即

(k为常数）

比较性

性质3如果在区域D上有f(x,y)≦g(x,y)，则

性质4 如果在有界闭区域D上f(x,y)=k（k为常数)，σ为D的面积，则Sσ=k∫∫dσ=kσ。