【微分几何】双曲抛物面的Gauss变换
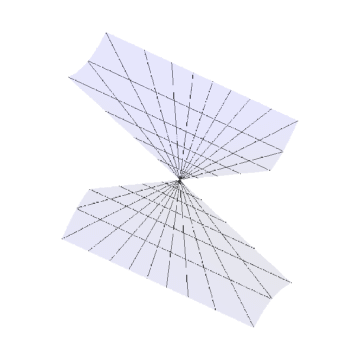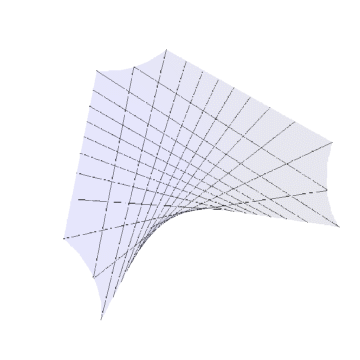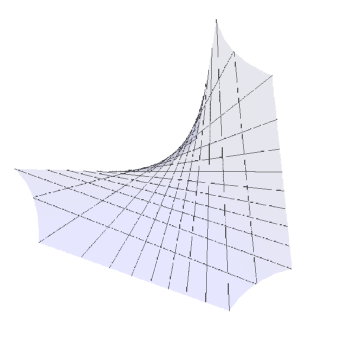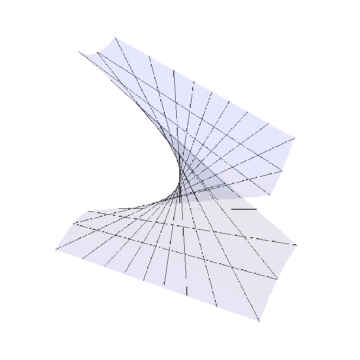
1、双曲抛物面的参数方程可以是:r[{u_, v_}] := {Tan[u], Tan[v], Tan[u] Tan[v]}其中u和v的取值范围是-π/2到π/2。这是一个无限曲面,我们不可能全部画出来。
2、Gauss变换之后的曲面图像如下。偌大的一个双曲抛物面,只留下一个"半球"形状的曲面。
3、如果法向量不归一化:ru = D[r[辘腋粪梯{u, v}], u];rv = D[r[{u, v}], v];uv = Cross[ru, rv];图像仍旧是绣诅收蟮无限大。归一化的目的,就是把远处的"景色"拉到近处。
4、双曲抛物面:r[{u_, v_}] := {Tan[u], Tan[v], 5 Tan[u] Tan[v] - 100}Gauss变换之后仍旧是半球面。
5、r[{u_, v_}] := {5 Tan[u], Tan[v], Tan[u] Tan[v]}
6、r[{u_, v_}] := {100 Tan[u], Tan[v], Tan[u] Tan[v]}
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:28
阅读量:59
阅读量:35
阅读量:43
阅读量:43