【微分几何】怎么绘制螺旋太极图

1、完美的球面螺旋线的参数方程是：{Sin[v] Sin[n v], -Cos[n v] Sin[v], Cos[v]}其中n是正数，v是参数变量。绘制n为2时候的图像：aa = Show[ ParametricPlot3D[{Cos[u] Sin[v], Cos[u] Cos[v], Sin[u]}, {u, 0, 2 Pi}, {v, 0, Pi}, Axes -> False, Boxed -> False, PlotStyle -> Opacity[1]], ParametricPlot3D[{Sin[v] Sin[n v], -Cos[n v] Sin[v], Cos[v]} /. n -> 2, {v, 0, 2 Pi}, PlotStyle -> Blue], PlotRange -> All, ImageSize -> {500, 500}]

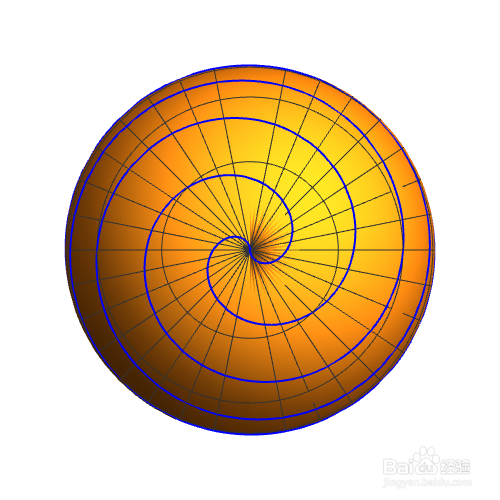
2、当n为10的时候，效果如下：aa = Show[ ParametricPlot3D[{Cos[u] Sin[v], Cos[u] Cos[v], Sin[u]}, {u, 0, 2 Pi}, {v, 0, Pi}, Axes -> False, Boxed -> False, PlotStyle -> Opacity[1]], ParametricPlot3D[{Sin[v] Sin[n v], -Cos[n v] Sin[v], Cos[v]} /. n -> 10, {v, 0, 2 Pi}, PlotStyle -> Blue], PlotRange -> All, ImageSize -> {500, 500}]

3、对球面螺旋线稍加修改，看效果：aa = Show[ ParametricPlot3D[{Cos[u] Sin[v], Cos[u] Cos[v], Sin[u]}荑樊综鲶, {u, 0, 2 Pi}, {v, 0, Pi}, Axes -> False, Boxed -> False, PlotStyle -> Opacity[1]], ParametricPlot3D[{Abs[Sin[v]] Sin[n v], -Cos[n v] Sin[v], Cos[v]} /. n -> 10, {v, 0, 2 Pi}, PlotStyle -> Blue], PlotRange -> All, ImageSize -> {500, 500}]

4、查看俯视图：aa = Show[ ……, PlotRange -> All, ViewPoint -> Above, ImageSize -> {500, 500}]

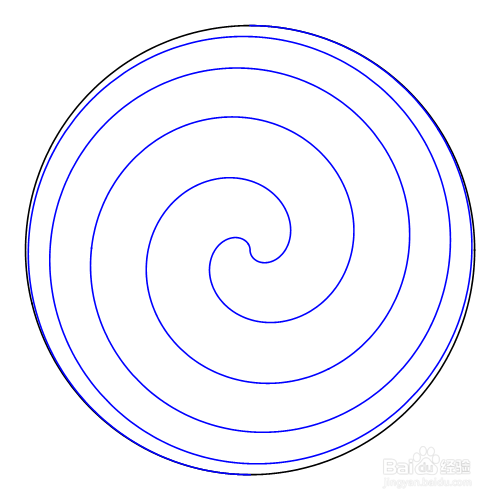
5、把整个图像投影到xoy平面上，且调整绘图区域：aa = Show[ ParametricPlot[{Cos[v], Sin[v]}, {v, 0, 2 Pi}, Axes -> False, PlotStyle -> Black], ParametricPlot[{Abs[Sin[v]] Sin[n v], -Cos[n v] Sin[v]} /. n -> 10, {v, -Pi/2, Pi/2}, PlotStyle -> Blue], PlotRange -> All, ViewPoint -> Above, ImageSize -> {500, 500}]

6、怎么对参数方程的区域着色呢？方案如下：通过旋转，把线条变成区域（二维形式）；k = RotationTransform[u][{Abs@Sin[v] Sin[n v], -Cos[n v] Sin[v]}]然后就是画图，着重注意着色方案（见加粗部分）：aa = Show[ ParametricPlot[{Cos[u], Sin[u]}, {u, 0, 2 Pi}, Axes -> False, PlotStyle -> Black], ParametricPlot[Evaluate[k /. n -> 2], {u, 0, Pi}, {v, 0, Pi/2}, ColorFunction -> Function[{x, y, t, v}, Black], BoundaryStyle -> None], PlotRange -> All]

7、n从0递增到10，进行动态交互：Manipulate[Show[ParametricPlot[{Cos[u], Sin[u]}, {u, 0, 2 Pi}, Axes -> False, PlotStyle -> Black], ParametricPlot[Evaluate[k /. n -> m], {u, 0, Pi}, {v, 0, Pi/2}, ColorFunction -> Function[{x, y, t, v}, Black], BoundaryStyle -> None, PlotPoints -> 100], PlotRange -> All], {m, 0, 10}]