用网络画板实现矩形在平面上滚动的动态课件

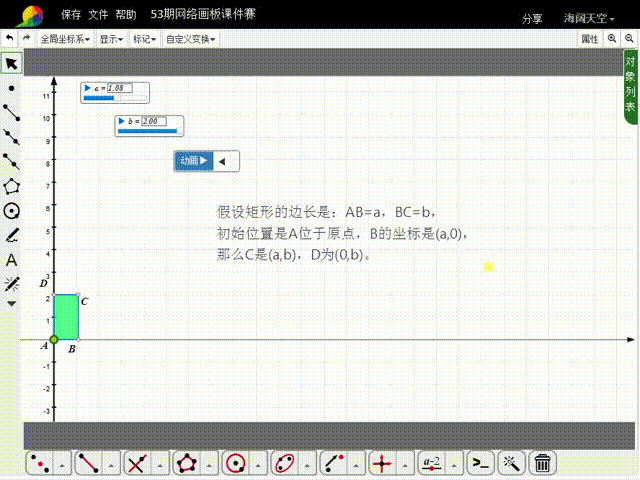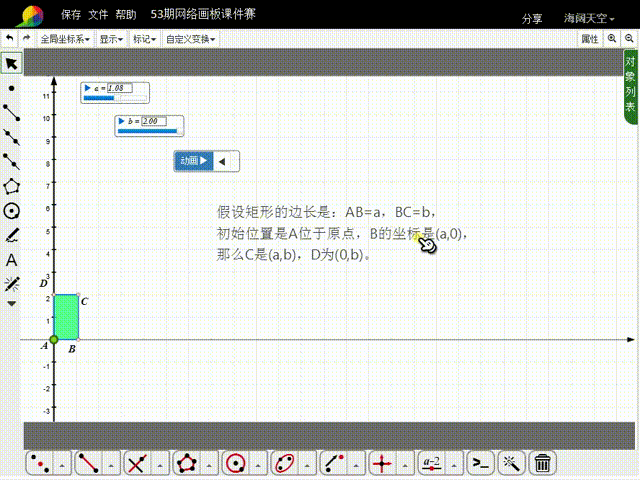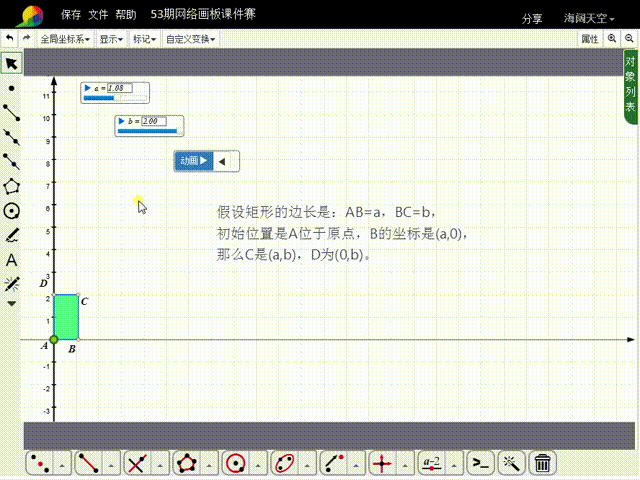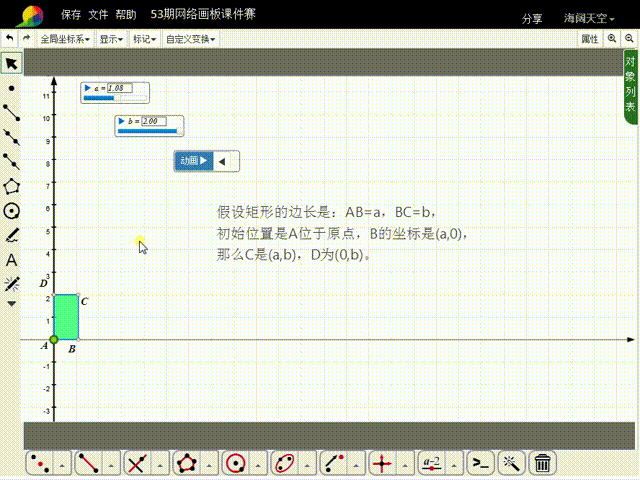
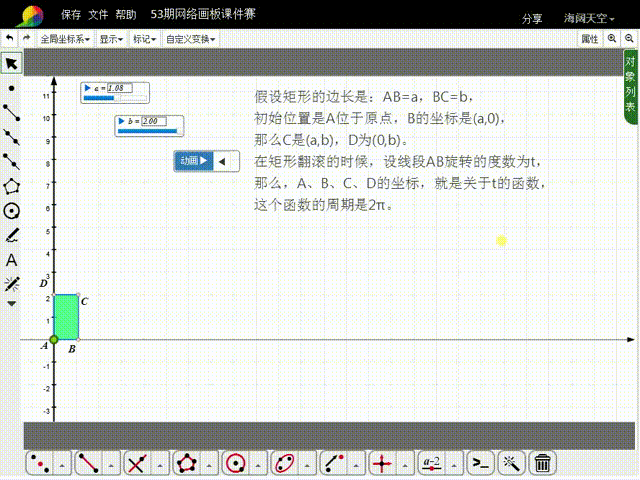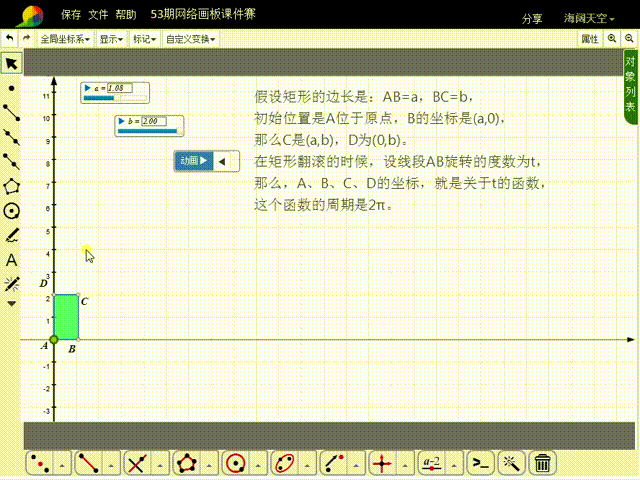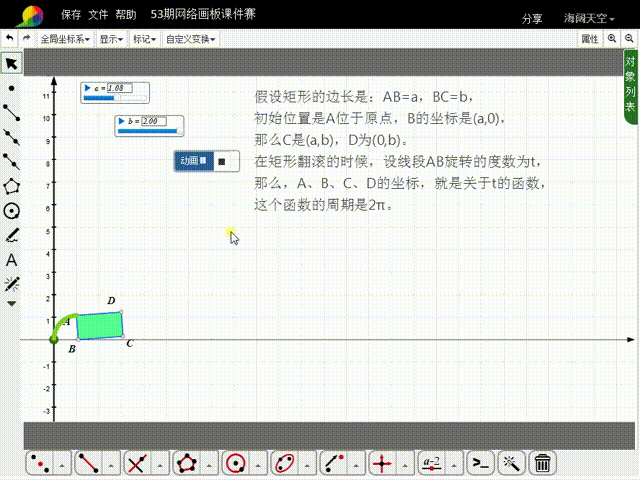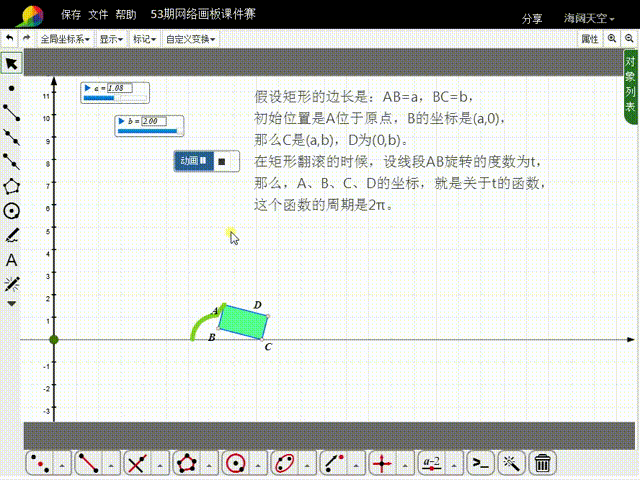
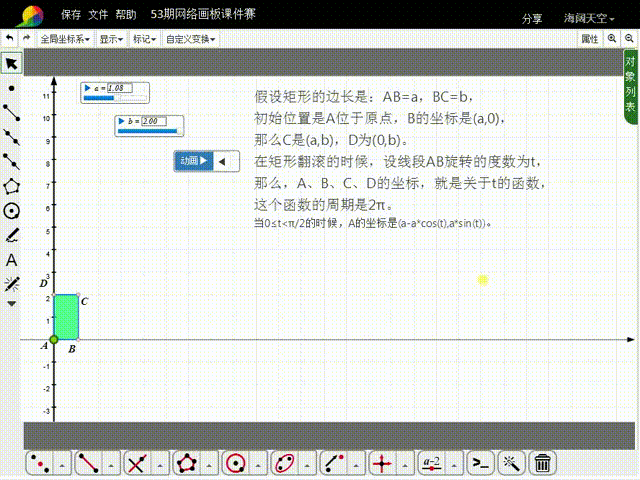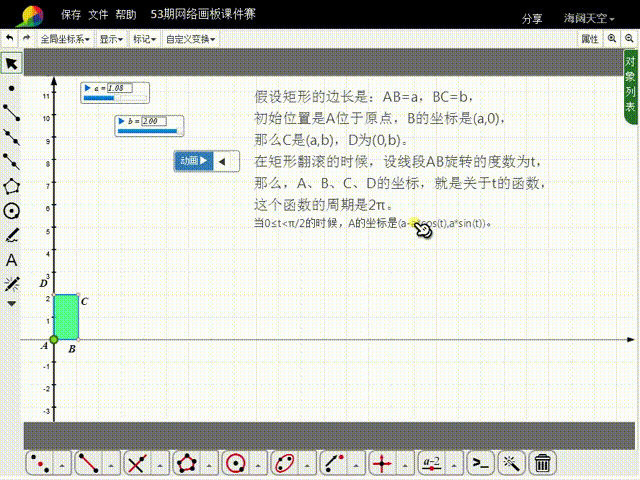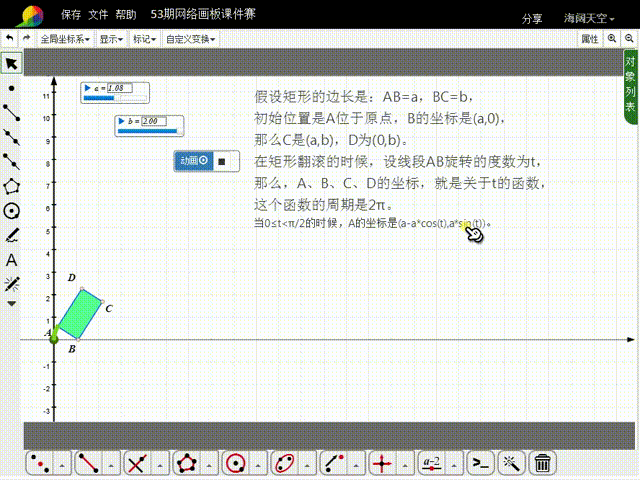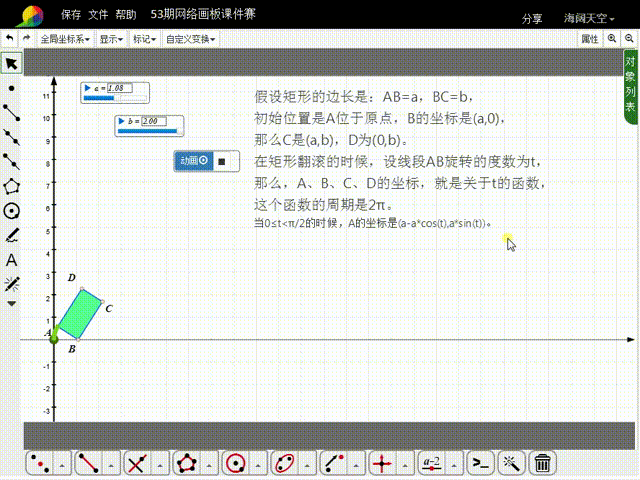
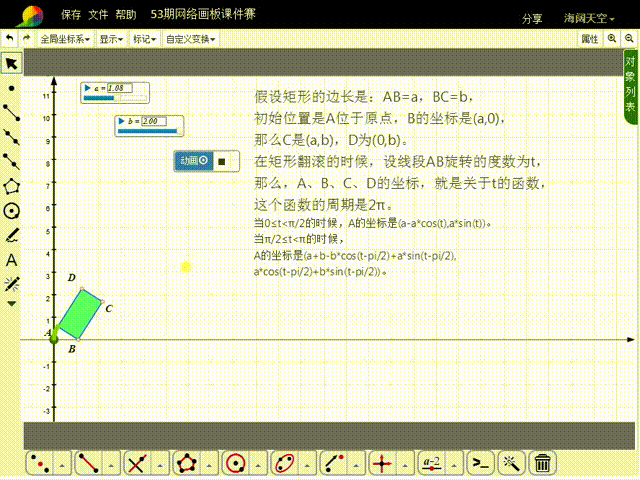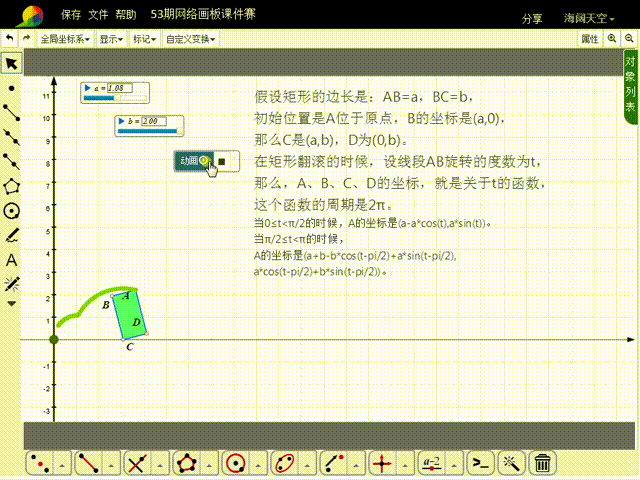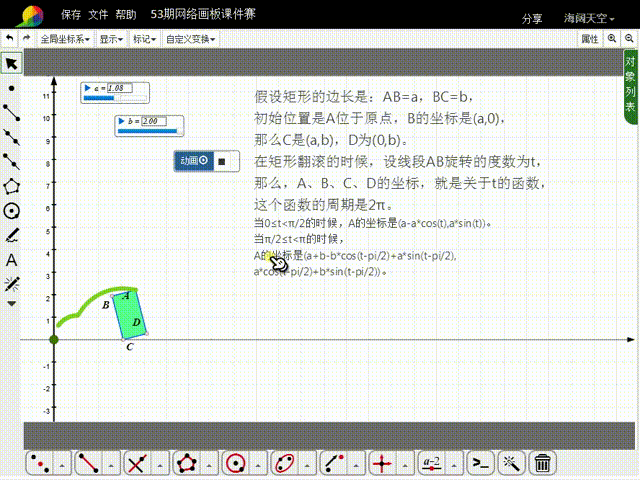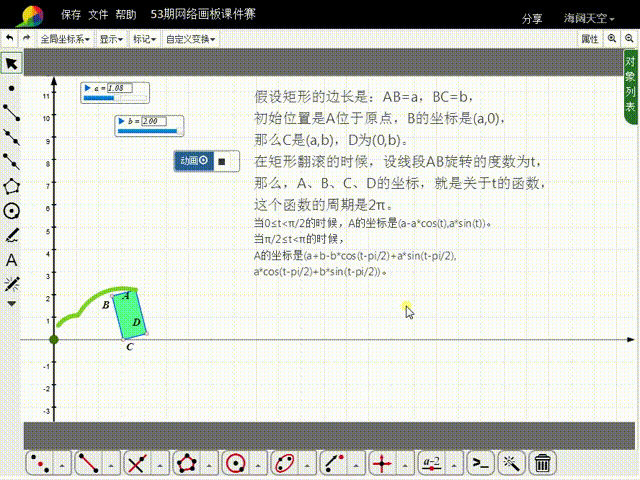
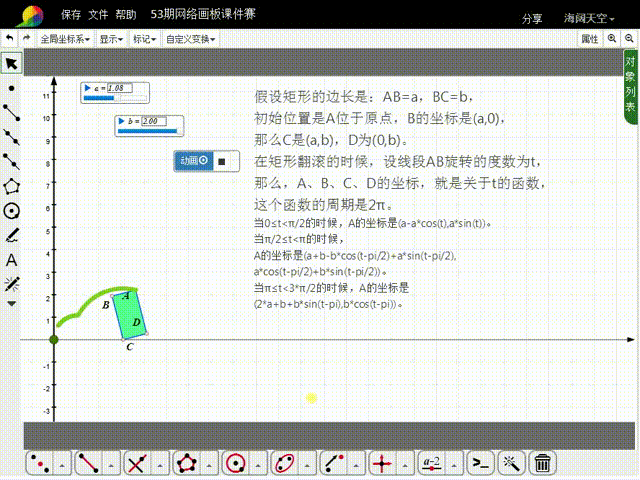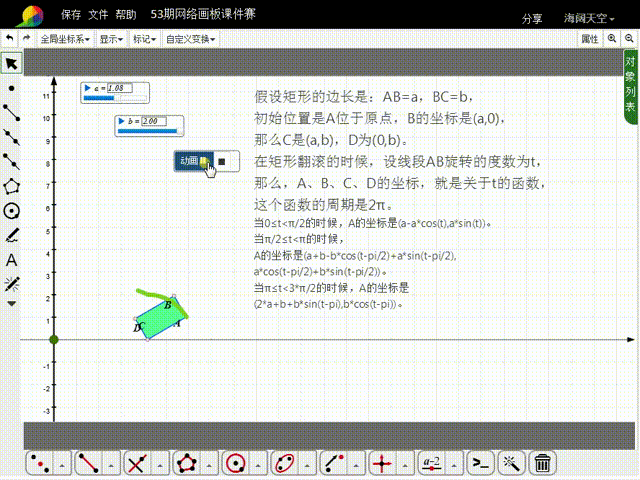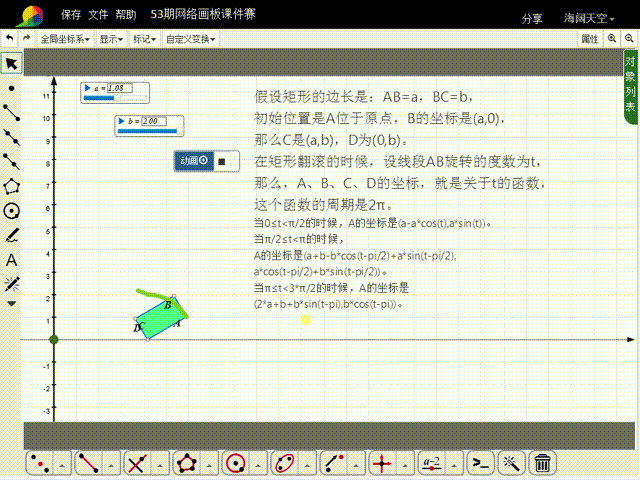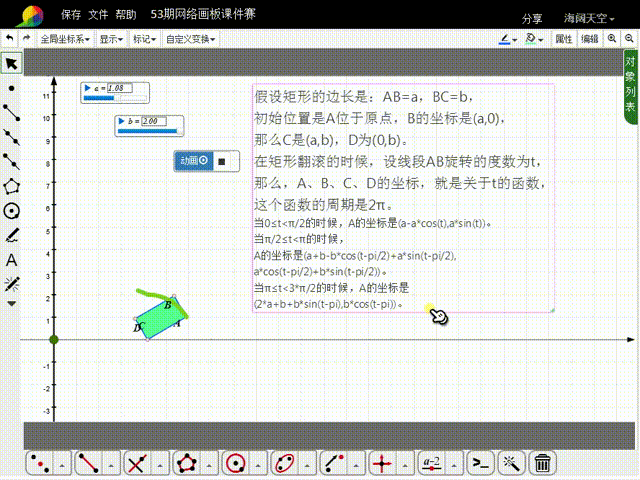
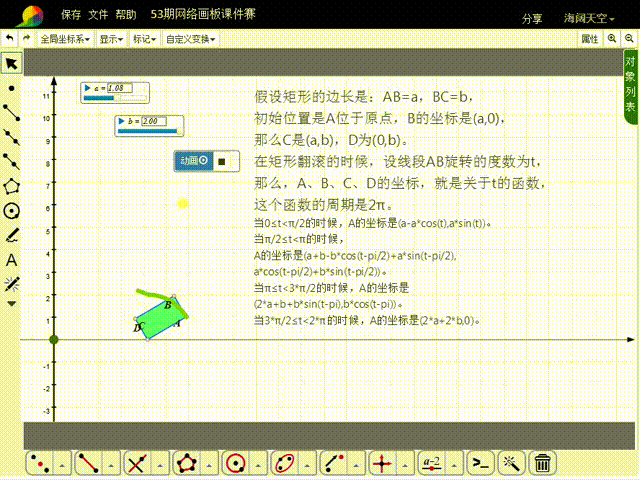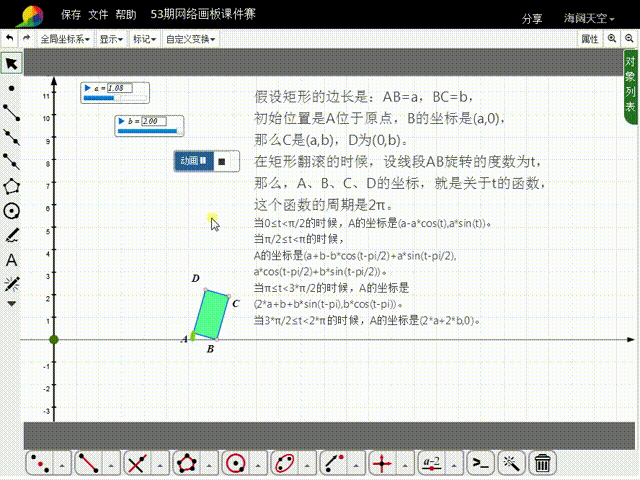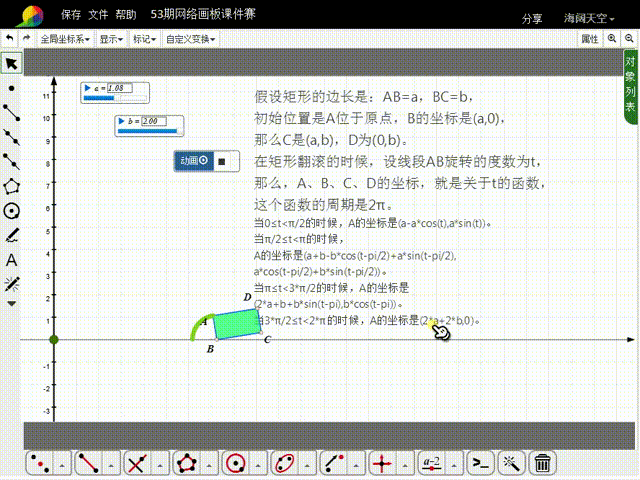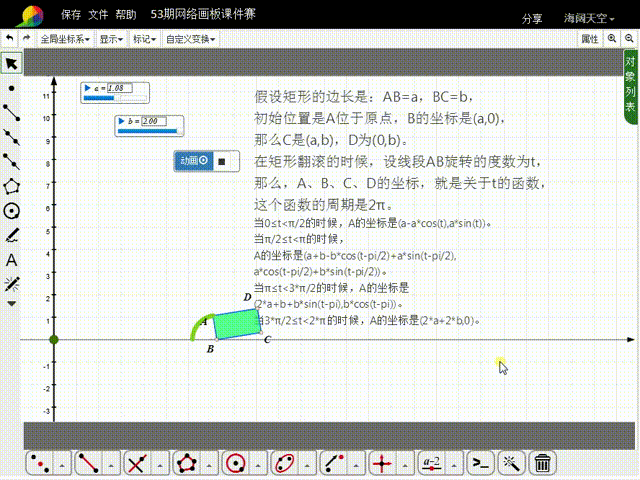
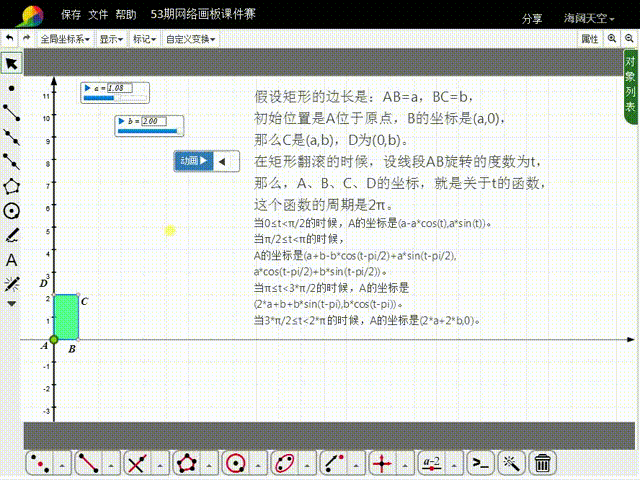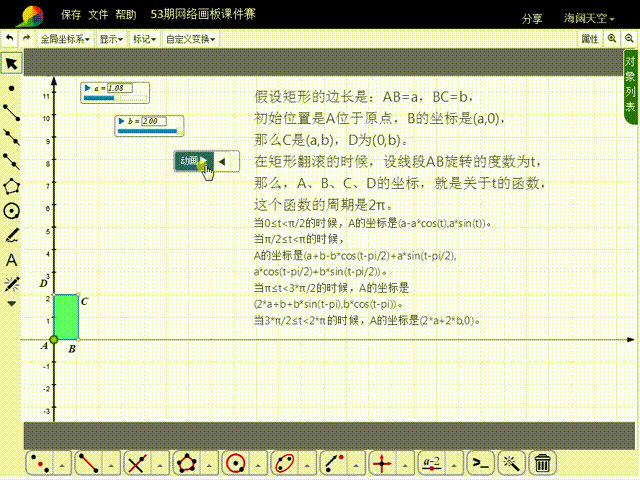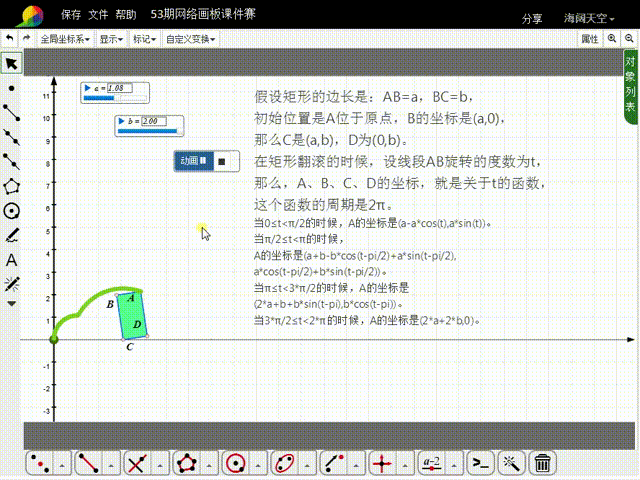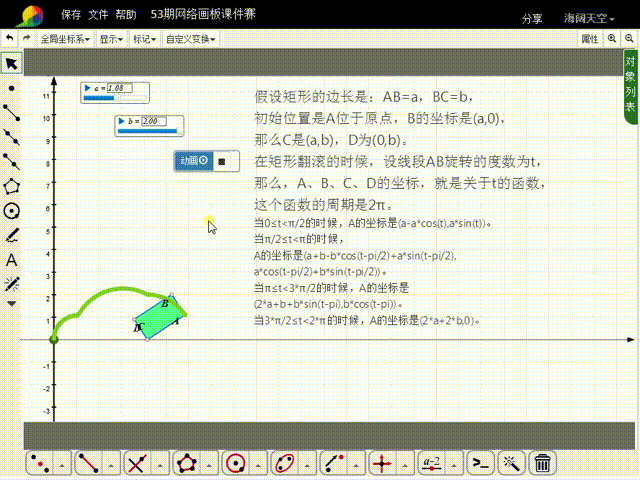
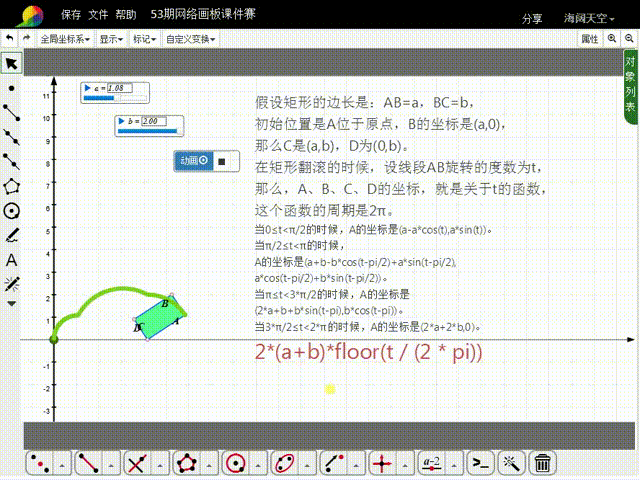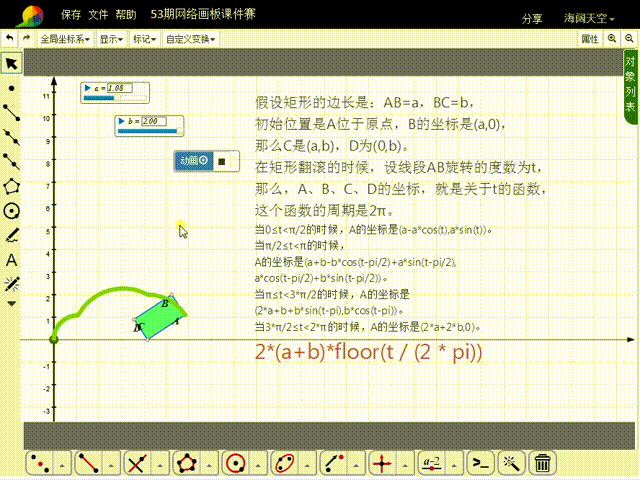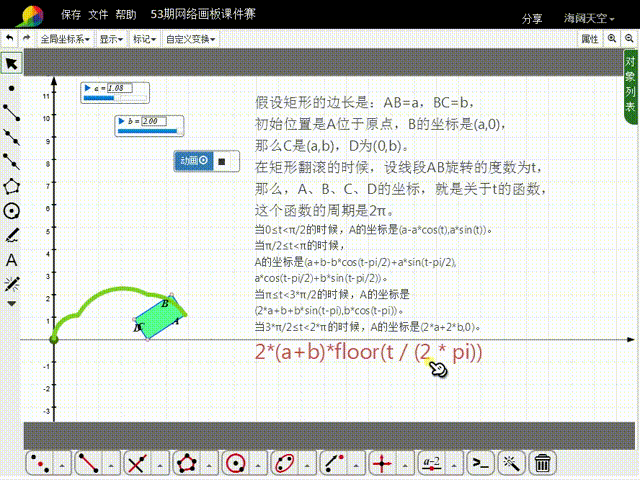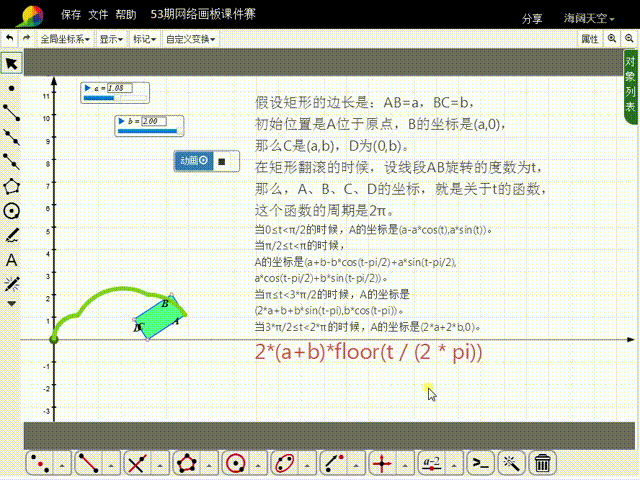
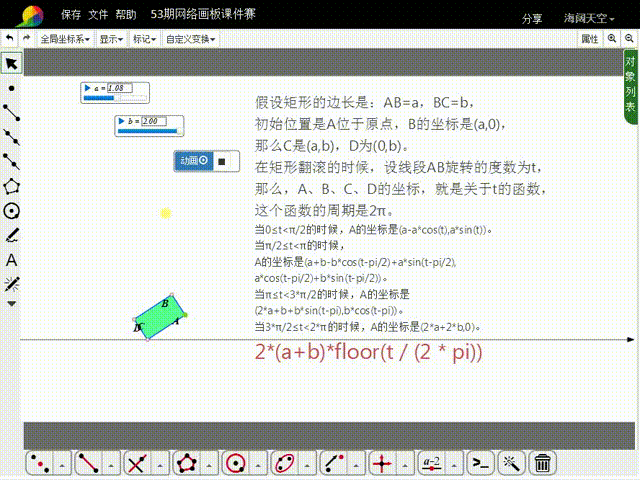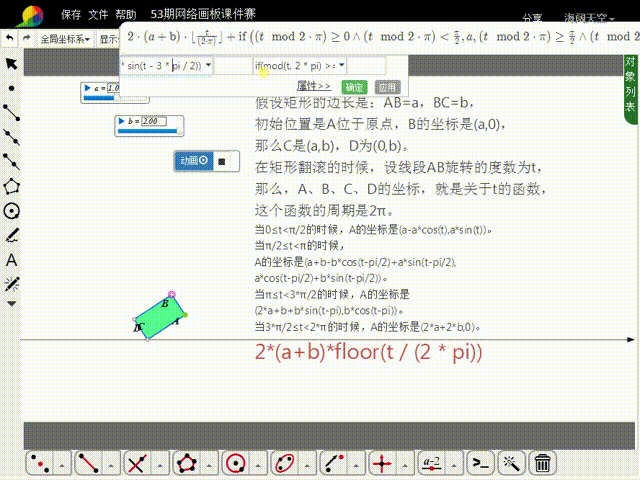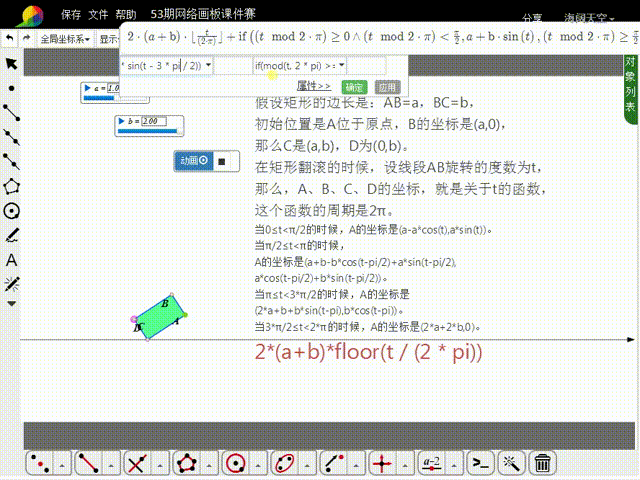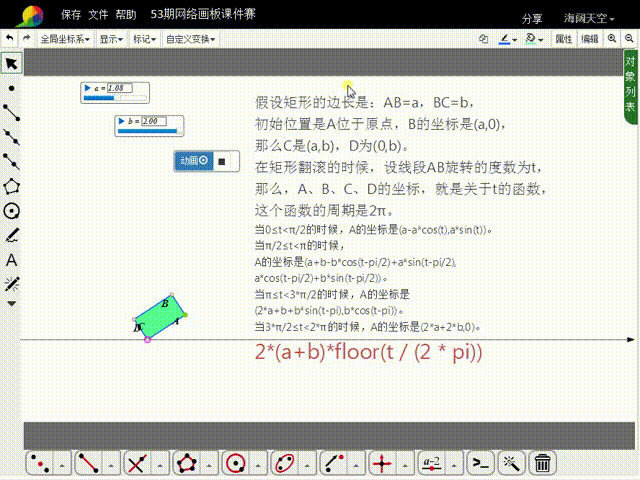
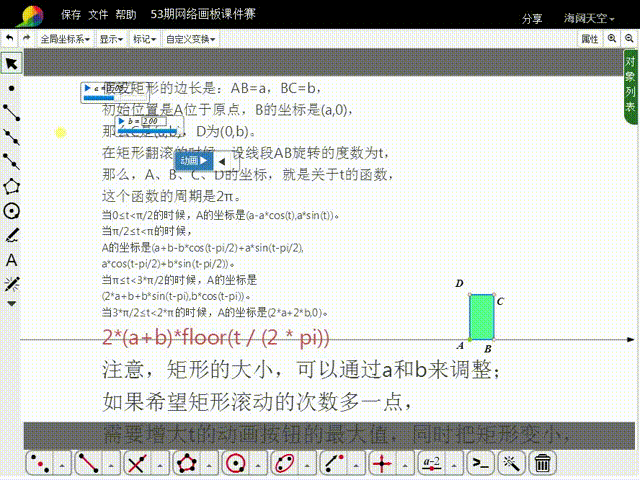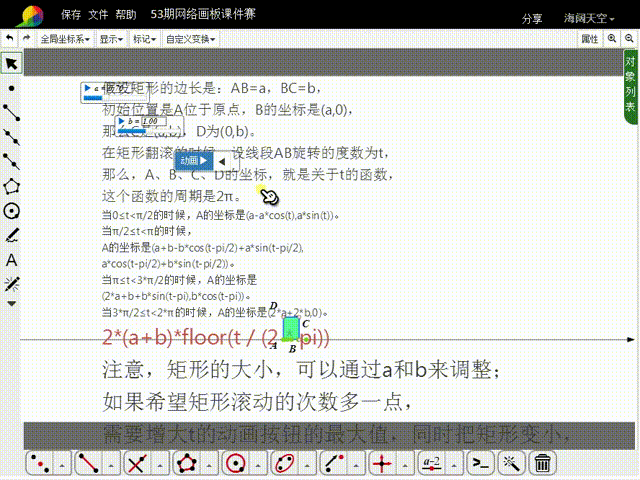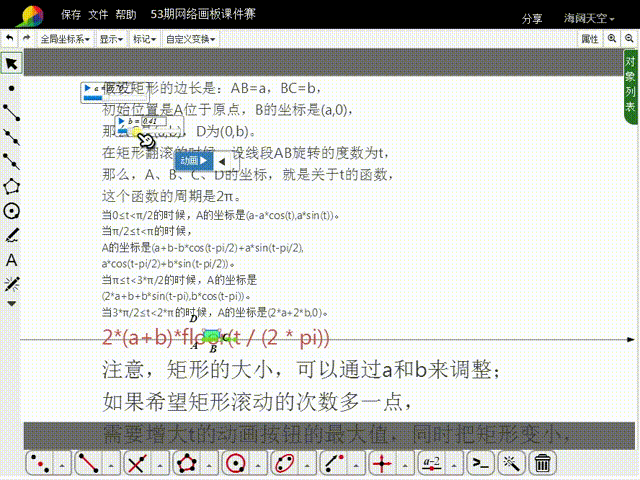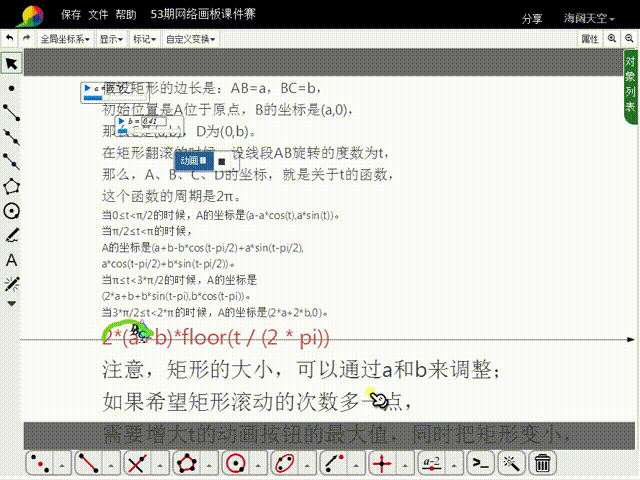
1、先来分析矩形的初始状态：假设矩形的边长是：AB=a，BC=b，初始位置是A位于原点，B的坐标是(a,0)，那么C是(a,b)，D为(0,b)。

2、在矩形翻滚的时候，设线段AB旋转的度数为t，那么，A、B、C、D的坐标，就是关于t的函数，这些函数的周期是2π。

3、当0≤t<π/2的时候，A的坐标是(a-a*cos(t),a*sin(t))。

4、当π/2≤t<π的时候，A的坐标是猾诮沓靥(a+b-b*cos(t-pi/2)+a*sin(t-pi/2),a*cos(t-pi/2)+b*sin(t-pi/2))，比较复杂了。

5、当π≤t<3*π/2的时候，A的坐标是(2*a+b+b*sin(t-pi),b*cos(t-pi))。

6、当3*π/2≤t<2*π的时候，A的坐标是(2*a+2*b,0)。

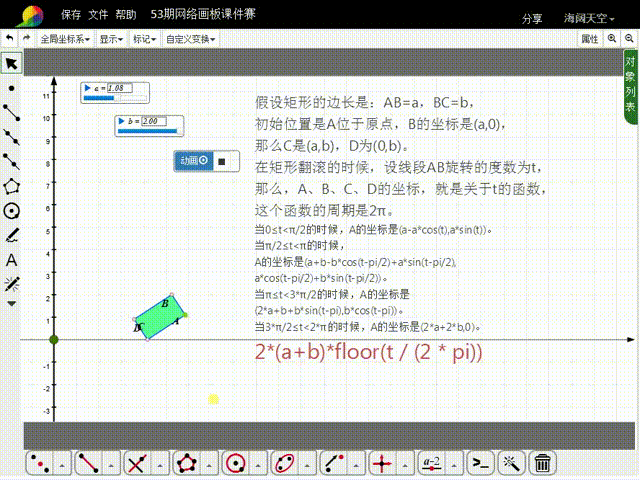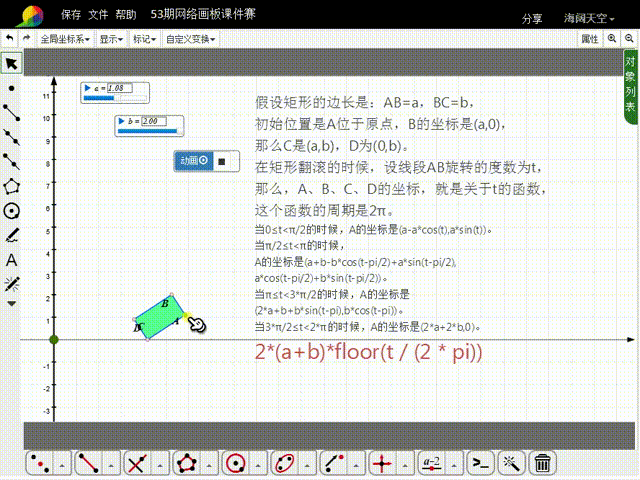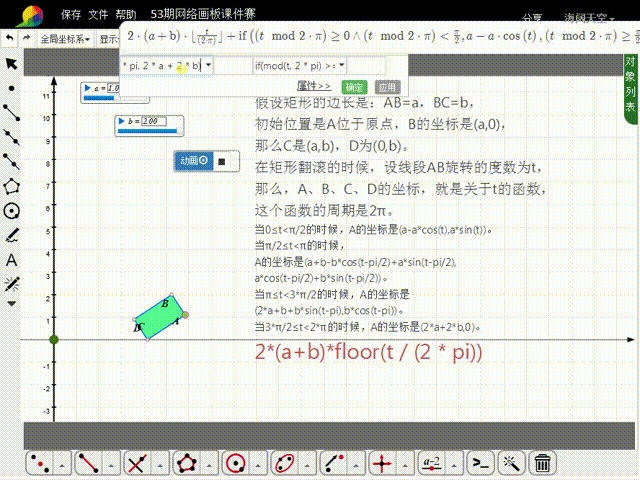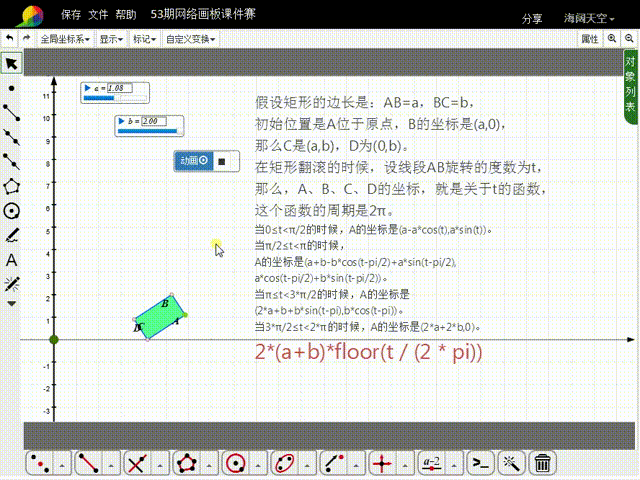
7、那么，在第一个周期内：A的横坐标为：if猾诮沓靥(mod(t, 2 * pi)>=0 and mod(t, 2 * pi)<pi/2,a-a*cos(t),mod(t, 2 忮氽阝另* pi)>=pi/2 and mod(t, 2 * pi)<pi,a+b-b*cos(t-pi/2)+a*sin(t-pi/2),mod(t, 2 * pi)>=pi and mod(t, 2 * pi)<3*pi/2,2*a+b+b*sin(t-pi),mod(t, 2 * pi)>=3*pi/2 and mod(t, 2 * pi)<2*pi,2*a+2*b)；A的纵坐标为：if(mod(t, 2 * pi)>=0 and mod(t, 2 * pi)<pi/2,a*sin(t),mod(t, 2 * pi)>=pi/2 and mod(t, 2 * pi)<pi,a*cos(t-pi/2)+b*sin(t-pi/2),mod(t, 2 * pi)>=pi and mod(t, 2 * pi)<3*pi/2,b*cos(t-pi),mod(t, 2 * pi)>=3*pi/2 and mod(t, 2 * pi)<2*pi,0)。

8、当AB的旋转角度大于2π的时候，A的横坐标需要加上：2*(a+b)*floor(t / (2 * pi))，而纵坐标的函数式保持不变。

9、这样，就可以用a、b、t来表示出每一刻A的坐标：A的横坐标为：2*(a+b)*floor(t / (2 * pi))+if(mod(t, 2 * pi)>=0 and mod(t, 2 * pi)<pi/2,a-a*cos(t),mod(t, 2 * pi)>=pi/2 and mod(t, 2 * pi)<pi,a+b-b*cos(t-pi/2)+a*sin(t-pi/2),mod(t, 2 * pi)>=pi and mod(t, 2 * pi)<3*pi/2,2*a+b+b*sin(t-pi),mod(t, 2 * pi)>=3*pi/2 and mod(t, 2 * pi)<2*pi,2*a+2*b)；A的纵坐标为：if(mod(t, 2 * pi)>=0 and mod(t, 2 * pi)<pi/2,a*sin(t),mod(t, 2 * pi)>=pi/2 and mod(t, 2 * pi)<pi,a*cos(t-pi/2)+b*sin(t-pi/2),mod(t, 2 * pi)>=pi and mod(t, 2 * pi)<3*pi/2,b*cos(t-pi),mod(t, 2 * pi)>=3*pi/2 and mod(t, 2 * pi)<2*pi,0)。以此绘制直角坐标点A。

10、同样的，也可以用a、b、t来表示出每一刻的B、C、D的坐标。

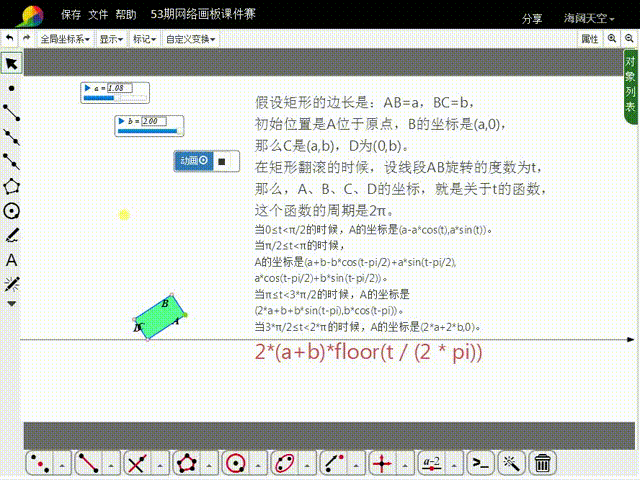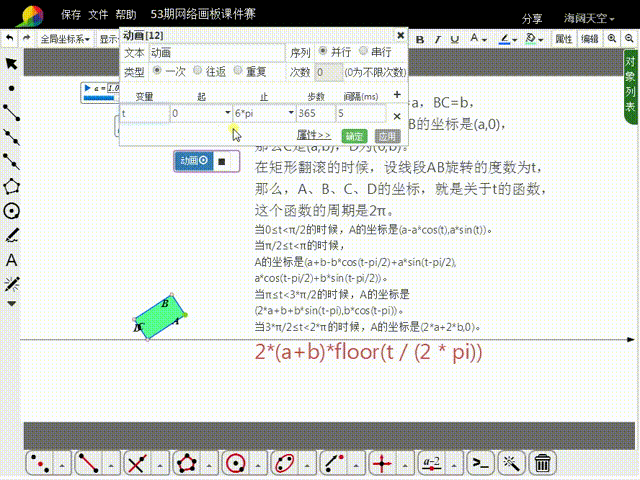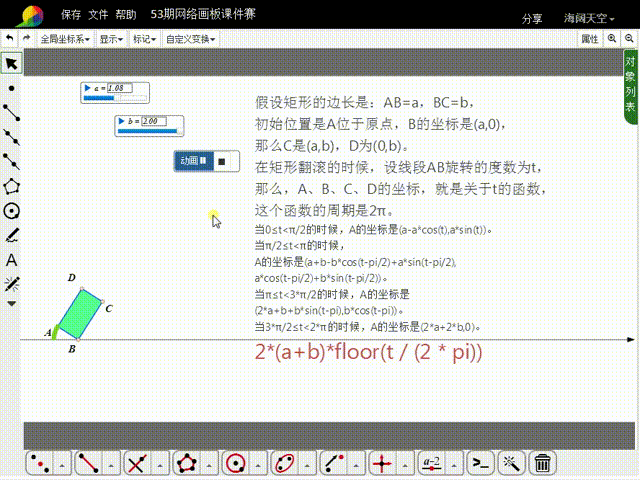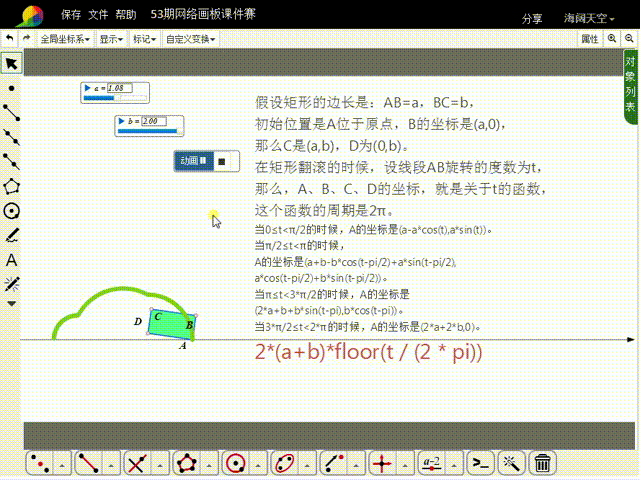
11、构造t的动画按钮，就可以实现矩形的滚动。

12、注意，矩形的大小，可以通过a和b来调整；如果希望矩形滚动的次数多一点，需要增大t的动画按钮的最大值，同时把矩形变小，否则矩形就会出界。