勾股定理的奥秘与证明

1、勾股定理的证明方法多种多样，下面介绍几种常见的证明方法：1. 欧几里得算法：这是最早证明勾股定理的方法之一，由古希腊数学家欧几里得提出。基本思想是通过构造两个正方形，一个以直角三角形的两条直角边为边长，另一个以斜边为边长，然后利用面积相等来证明勾股定理。具体证明过程涉及反证法和等面积法，通过一系列的逻辑推理，最终得出a² + b² = c²的结论。

2、2. 相似三角形法：这种方法基于相似三角形的性质来证明勾股定理。首先，在直角三角形中构造一个等腰直角三角形，使得其与原直角三角形的一条直角边重合。然后，通过证明两个三角形相似，并利用相似三角形的边长比例关系，最终推导出勾股定理。

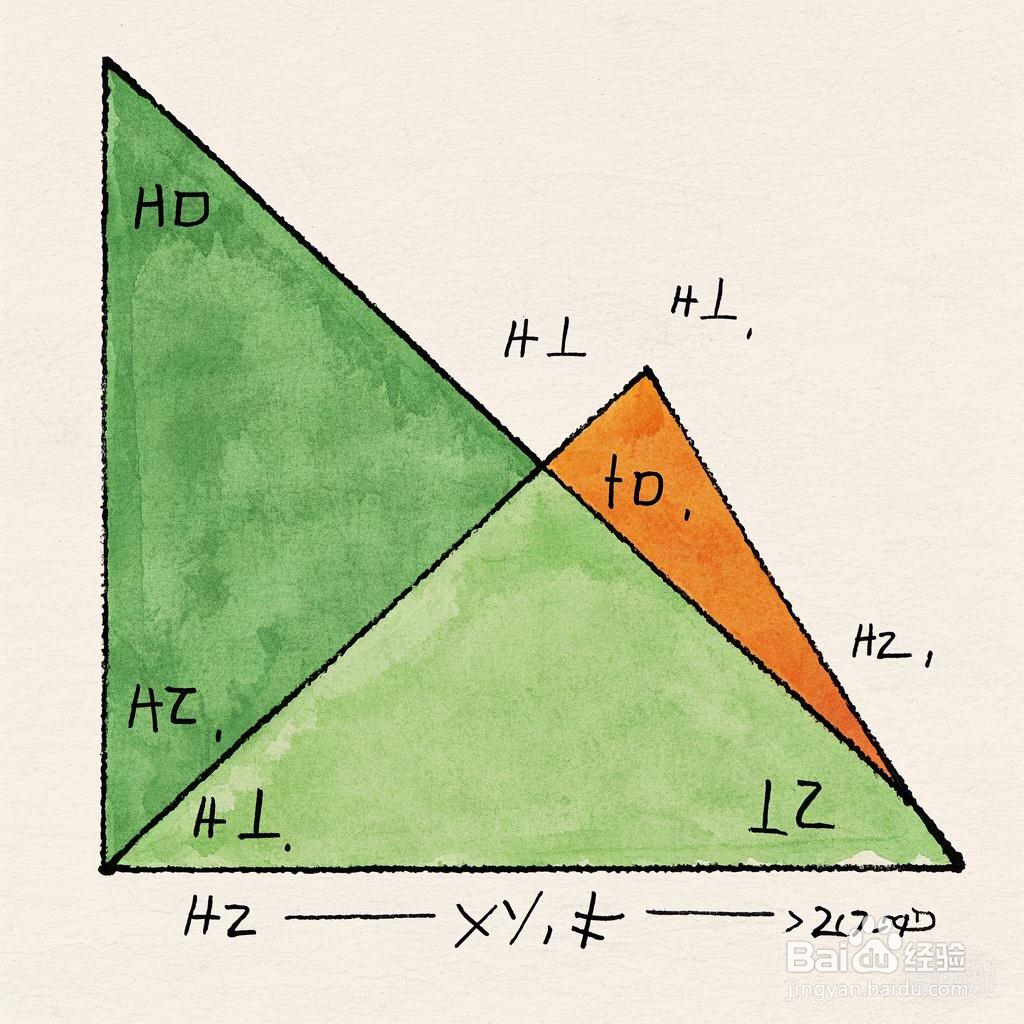
3、3. 赵爽弦图法：这是中国古代数学家赵爽提出的一种证明方法。他通过构造四个全等的直角三角形和一个正方形，然后利用面积关系来证明勾股定理。这种证明方法直观易懂，展示了中国古代数学家的智慧和创造力。

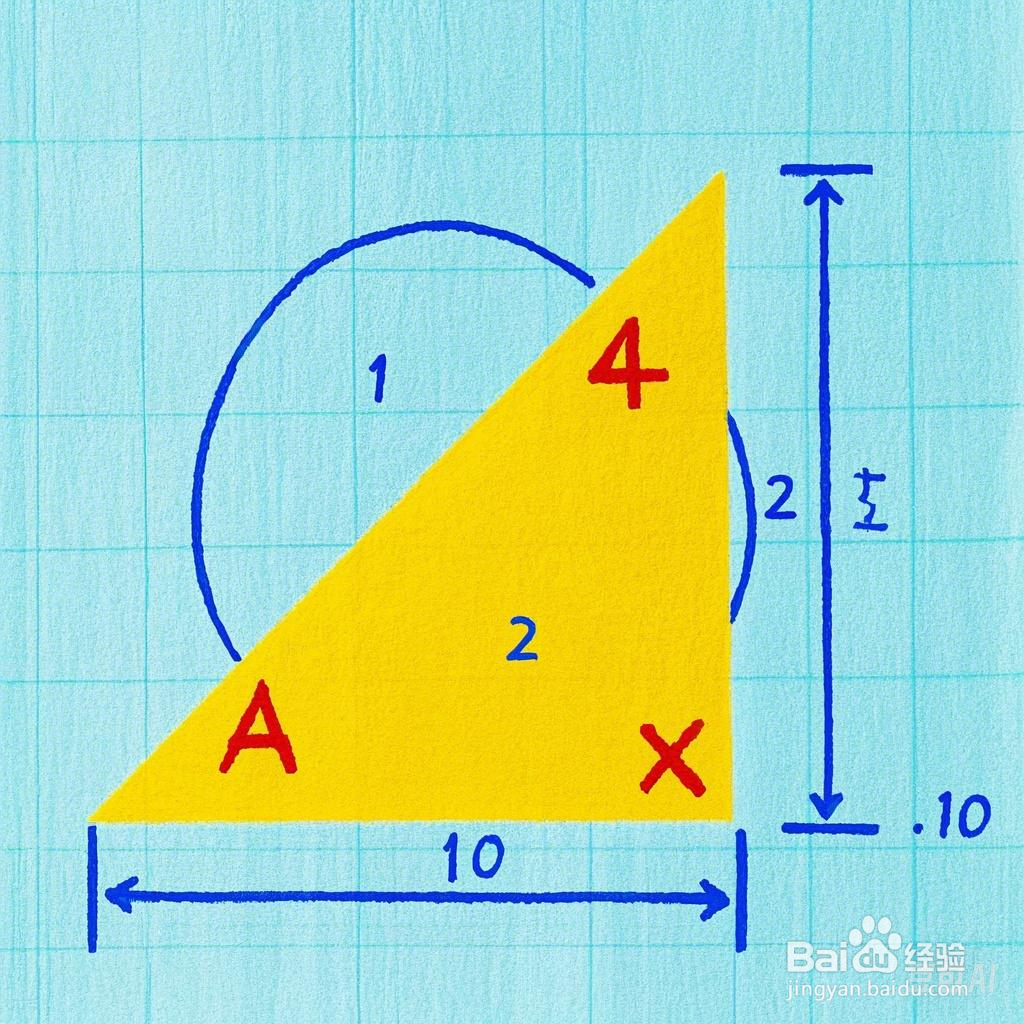
4、4. 总统证法：*美国加菲尔德曾给出一个巧妙的证明方法。 他利用梯形面积公式和等面积法，通过计算梯形的面积来证明勾股定理。这种证明方法简洁明了，易于理解。