线性同余方程组（Mathematica）

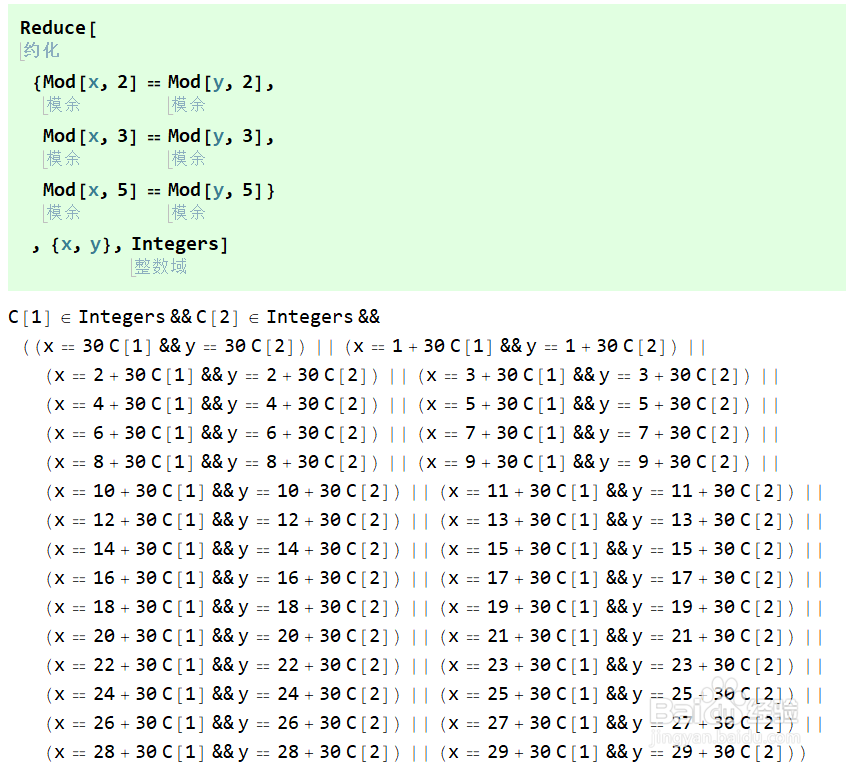
1、首先，如果两个墙绅褡孛数，模a,b,c同余，那么它们模(a,b,c)同余。且模(a,b,c)同余可以表示所有解。使用Reduce化简同余方程，指定域为Integers整数域。

2、为了使得结果简洁，我们设成x≡x+y(mod 2,3,5)，这样Reduce以后，使用Simplify化简，就只有一项。可见，y是30的倍数。

3、此处还可以使用Solve求解。得到的是条件表达式。Solve的结果使用/.替换，并带入C[1]即可以得到数值结果。

4、下面，我们说只有一个变量的同余方程组，比如如图的方程组，各个模数是互素的。使用Reduce直接得出结果为23(mod 105)

5、下面说分步求解过程：首先使用LCM求得各个模数的最小公倍数，除以各个模数，得到M1,M2,M3。最终的结果是M1,M2,M3的线性组合。

6、接下来，求解如图三个互相无关的线性同余方程。茧盯璜阝就是依次把原来方程中的x换成a*M1+b*M2+c*M3，然后消去无关项，个个方程就独立了。得到如图3个方程。分别求解出a,b,c。

7、这里，C[1]带入任意数都可。带入0比较好算。得到a=1,b=3,c=2。然后计算a*M1+b*M2+c*M3，得到128为原来线性同余方程组的一个解。

8、最后，对这个解模LCM[3,5,7]，即三个模数的最小公倍数105，得到解的形式为x≡23 (mod 105)

9、如图，演示了带入常数为C[1]=1，最终模完仍然是23。故常数C[1]无关紧要。

10、下面说模数不互素时的解决方法。首先，如图方程组为例，使用Reduce也可以直接求解。

11、根据第一个方程，设x=6t+4，带入第二个，求出t。

12、然后根据t求出x。解x模LCM(m1,m2)同余。如图，LCM(m1,m2)=24，故解为x≡10(mod 24)