【平面几何】怎么了解直线的垂心变换像

先给出定义，垂心反演变换给定线段AB，点C是直线A幞洼踉残B外任意点，△ABC的垂心记为D，那么，C到D的变换，称为关于线段AB的垂心变换，记为f(C)=D又因为f(D)=C，因此，这个变换是一种反演变换。本文，就来演示垂心变换。

工具/原料

电脑

Mathematica

网络画板

创建自定义变换

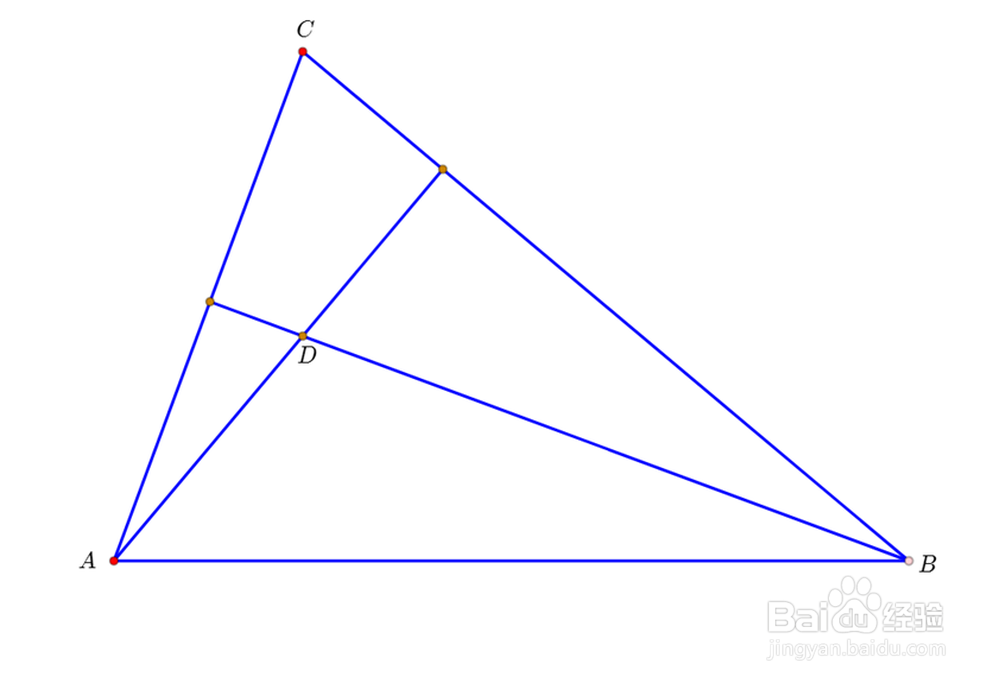
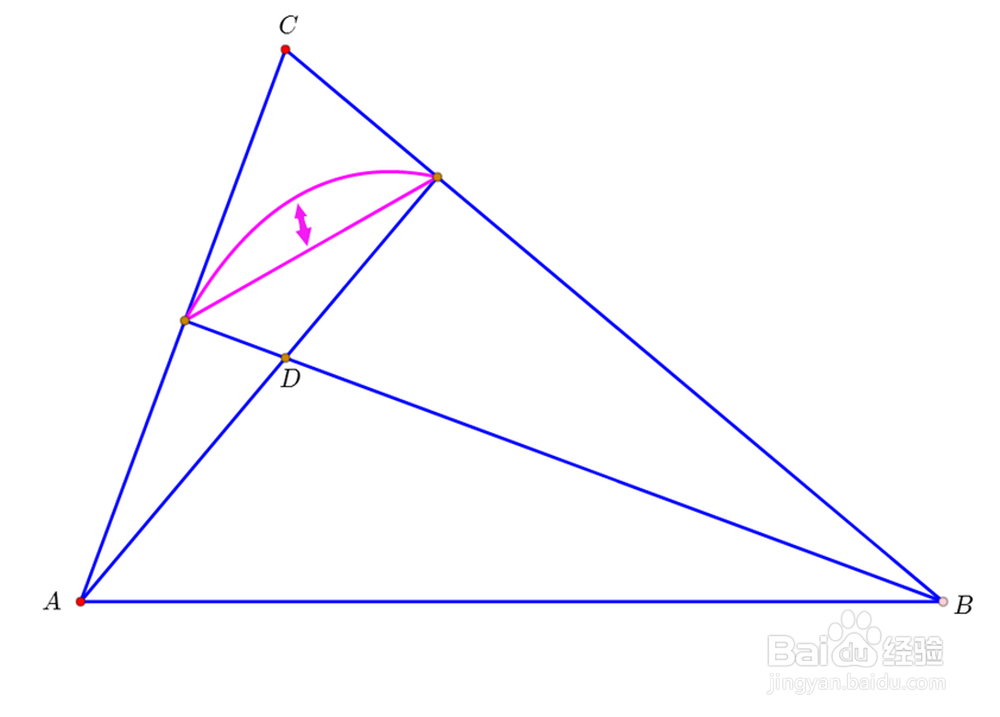
1、给定两定点A和B，连接直线AB。在直线外任取动点C，然后构造△ABC的垂心D。

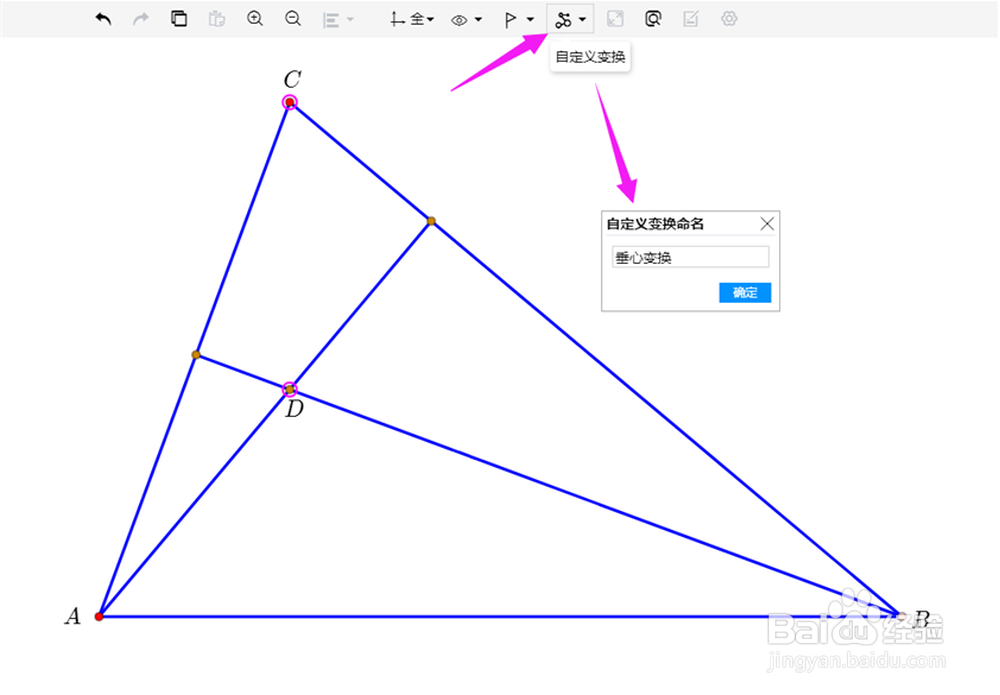
2、选中C和D，创建自定义变换，命名为【垂心变换】。

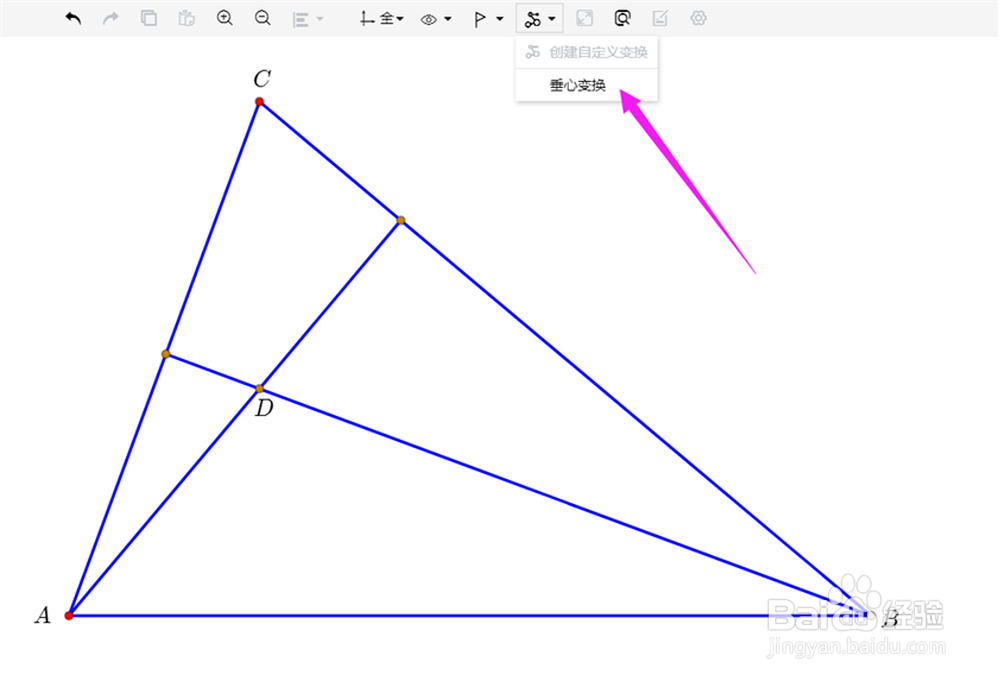
3、此时，在这个课件里面，就有了【垂心变换】工具了。

4、选择一个几何图形，再点击【垂心变换】工具按钮，就可以得到相应的变换像。这就是网络画板【自定义变换】功能的便捷之处。

直线的垂心变换像

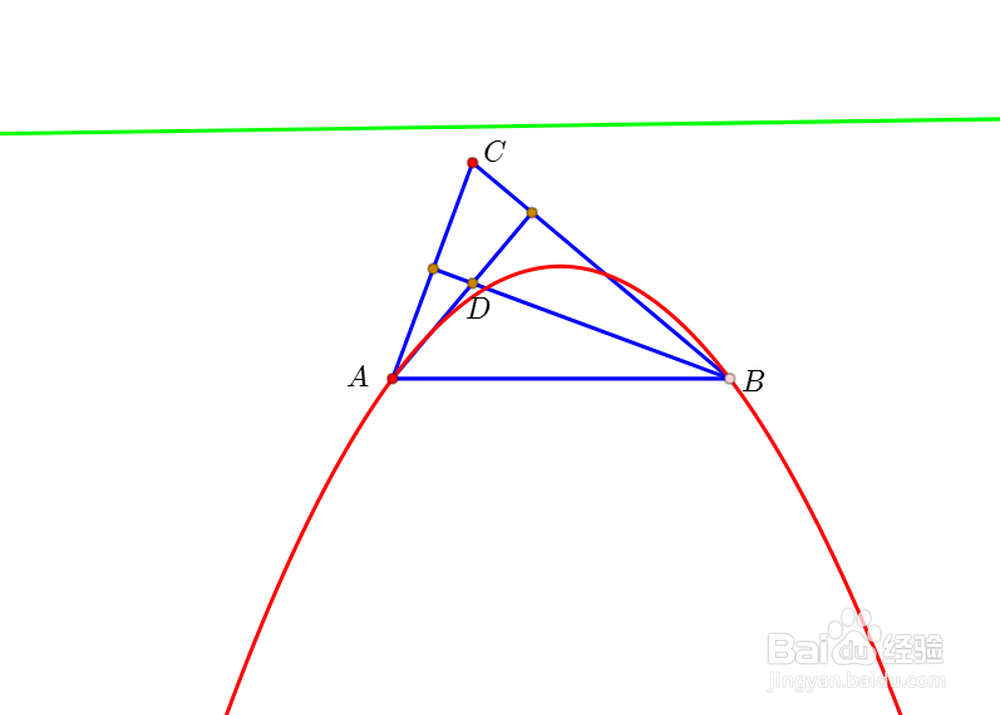
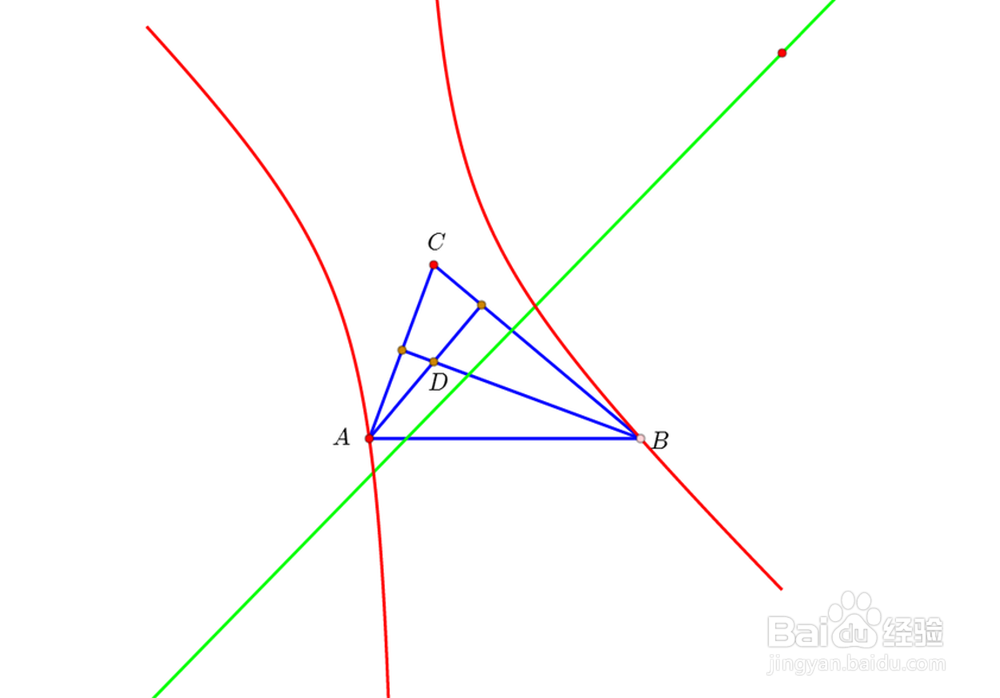
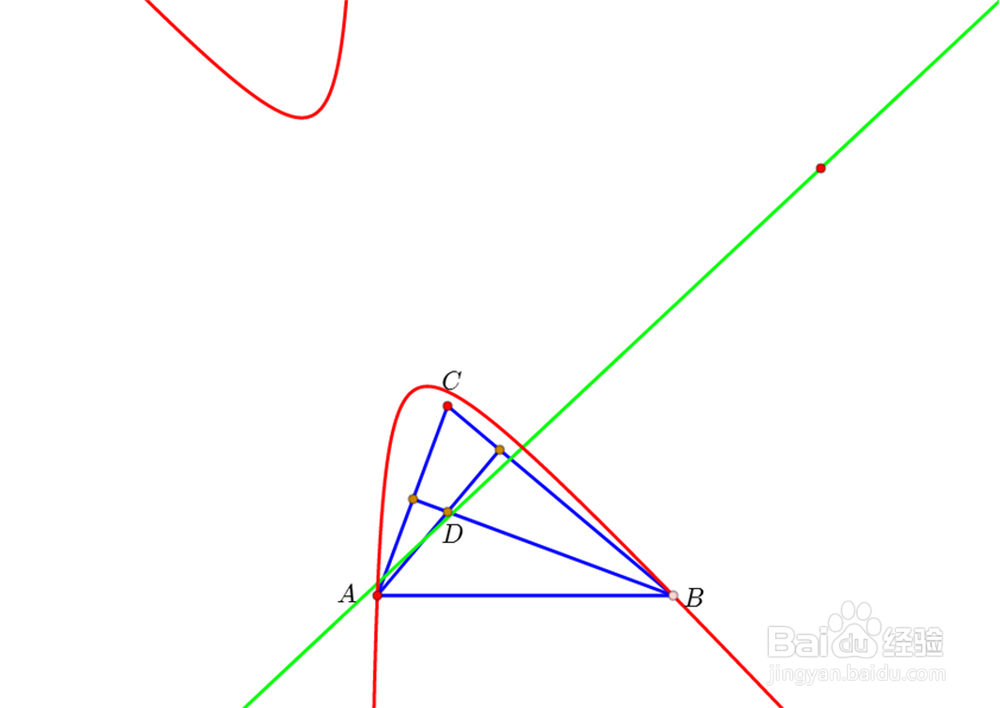
1、做任意不与直线AB重合的直线l（绿色），再构造直线l的垂心变换像（红色），可以发现，得到的曲线很像【双曲线】。

2、改变直线l的位置，【双曲线】的位置也随之改变。

定量分析

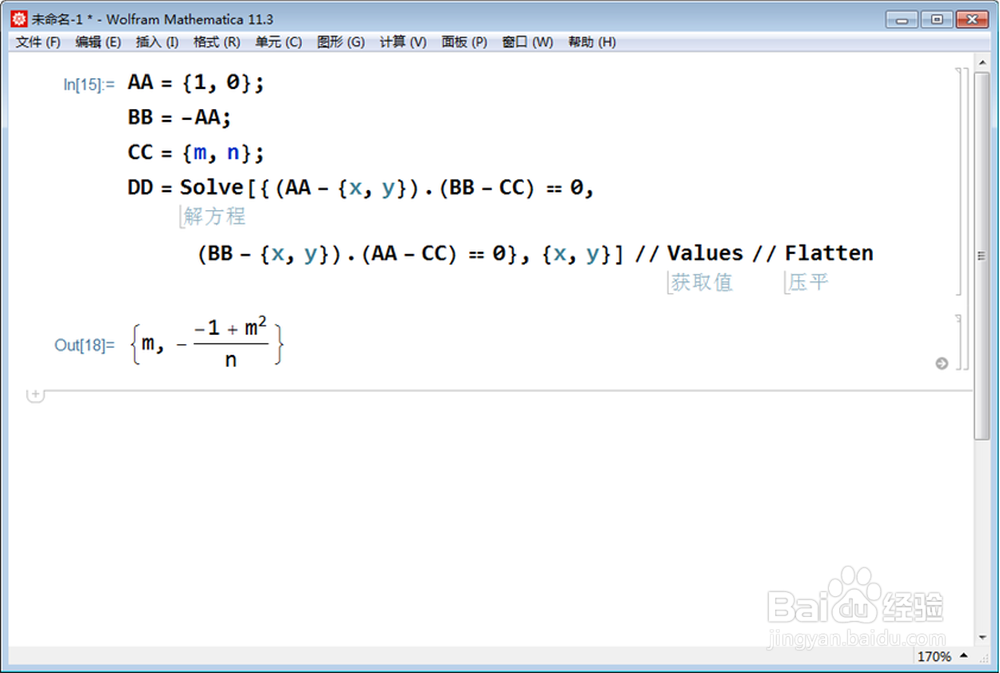
1、使用Mathematica进行符号计算，来确定直线的垂心变换像的参数方程。假设A和B的横坐标分别是±1，纵坐标是0，C的坐标是{m,n}，求出D的坐标。DD = Solve[{(AA - {x荑樊综鲶, y}).(BB - CC) == 0, (BB - {x, y}).(AA - CC) == 0}, {x, y}] // Values // Flatten。

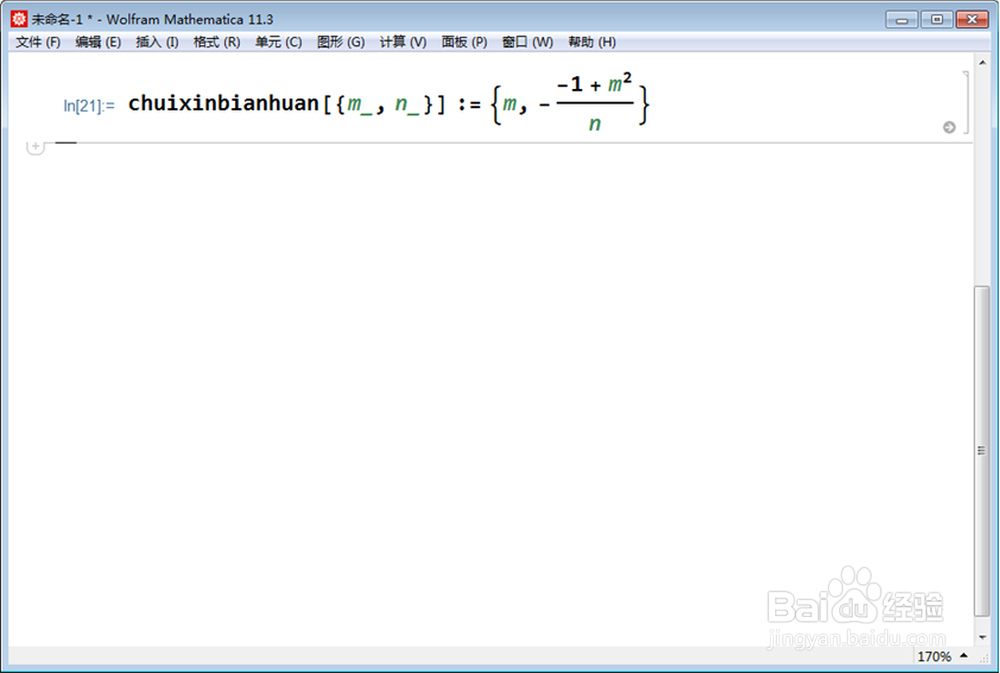
2、用自定义函数，写出【垂心变换】的变换规则。chuixinbianhuan[{m_, n_}] := {m, -((-1 + m^2)/n)}。

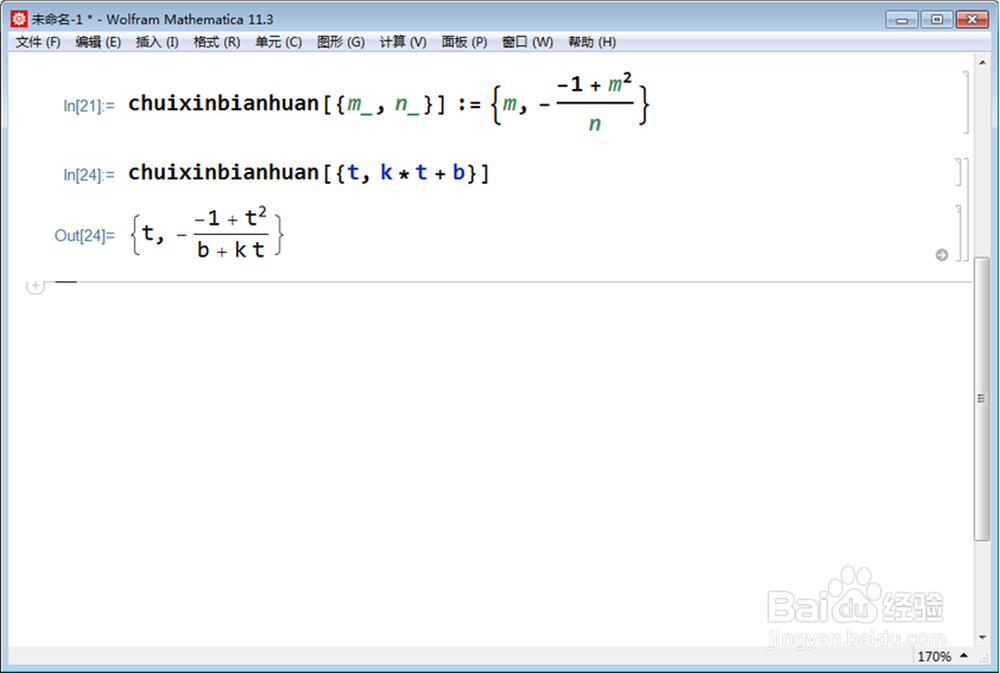
3、对直线y=k*x+b进行【垂心变换】，需要用到直线的参数方程。chuixinbianhuan[{t, k*t + b}]。得到的是变换像的参数方程。

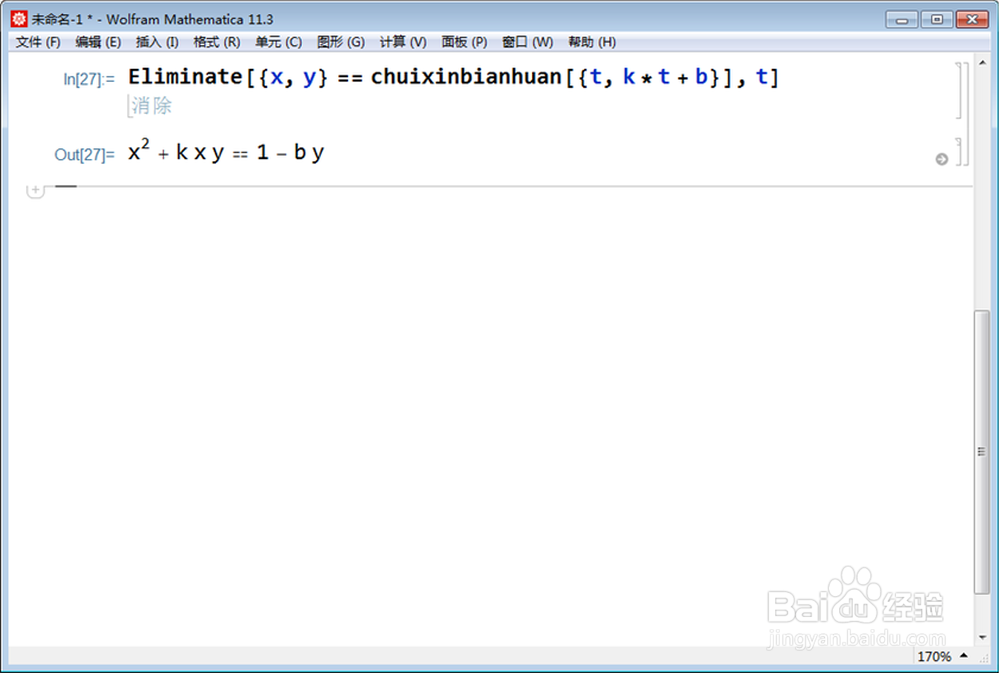
4、消去参数t，算出变湍恬擒舍换像的隐函数方程。Eliminate[{x, y} == chuixinbianhu锾攒揉敫an[{t, k*t + b}], t]。方程式是：x^2 + k x y == 1 - b y（k和b不全为0，否则直线y=k*x+b就与直线AB重合）。缺少y的二次项，显然不会是椭圆；如果k=0，那就是抛物线，否则就是双曲线。