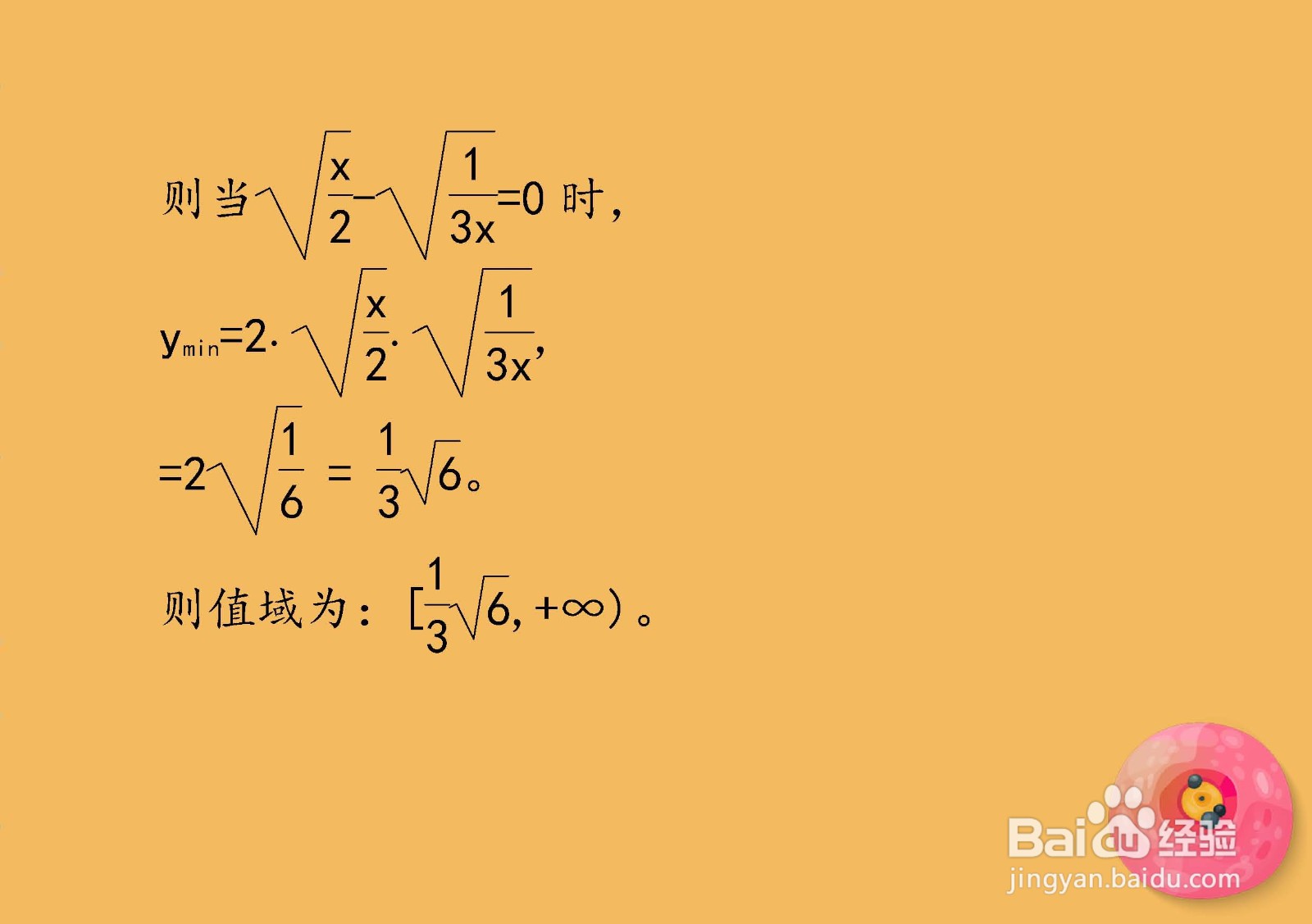如何求函数y=x/2+1/3x的值域

1、 通过二次方程判别式法、基本不等式法、配方法、导数法等，介绍求函数y=x/2+1/3x在x>0时值域的主要过程与步骤。

2、二次函数判别式法,将函数变形为x的二次函数，再利用二次方程判别式计算求解函数的值域。

3、由二次判别式有根，则判别式为非负数，即可求出参数的最小值，进而求出所求函数的值域。

4、基本不等式法，对任意两稍僚敉视个正数a,b，有基本不等式a+b≥2ab 。对于本题，有：y=x/2+1/3x ≥2√(1/2x*1/3x ) ,=2√(1/6) =√6/3.则值域为：[√6/3,+∞)。

5、均值不等式，又称为平均值不等式、平均不等式，是数舌哆猢筢学中的一个重要公式。公式内容为Hn≤Gn≤An≤Qn，即调和平均数不超过几何平均数，几何平均数不超过算术平均数，算术平均数不超过平方平均数。

6、将所求函数配方成为含有x的二次方程，再根据二次函数的性质求解值域。

7、根据条件，求出符合条件的自变量值，代入即可得到函数的最小值。

8、用导数求出函数的驻点，在判断函数的单调性，进而求出函数的最值，最终得到函数的值域。