用matlab求解方程二次规划问题

1、开始第一步我们打开在电脑桌面找到matlab小程序，然后鼠标右击打开桌面上matlab程序，运行起来。由于不同人电脑的配置不一样，软件打开的速度也有所不同，一般固态硬盘比机械硬盘运行的要快好多。大家稍微等待一下。

2、我们为了便于保存数据，我们点击matlab左上角新建脚本命令，创建新的脚本，创建M文件，也便于程序的保存，我们可以将其保存在电脑的其他盘，以便于我们的寻找和使用，这也是比较常见的方式。

3、这是一个常见的二次规划的方程，有目标函数，有约束条件，让其在约束条件的情况下求其的最优解和最优值下面问题有五个约束条件求约束条件的最小值

4、首先我们将方程里面的数值以矩阵的形式表示出来具体情况如下

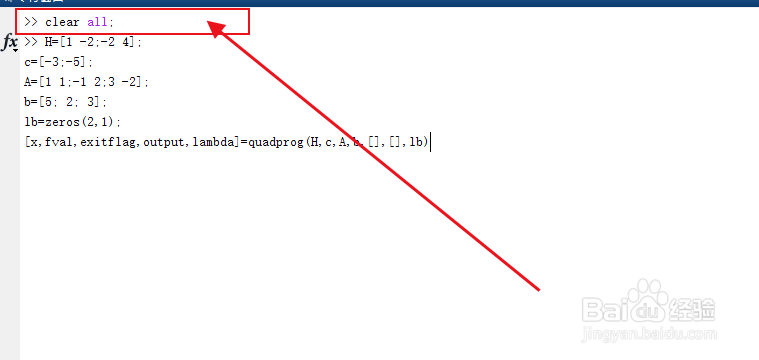
5、在新建脚本命令输入窗口输入程序>>clear all;注意书写的方式哦关闭所有正在运行的matlab程序，以便于我们的程序的运行和使用也可以让我们得到的结果更加的准确

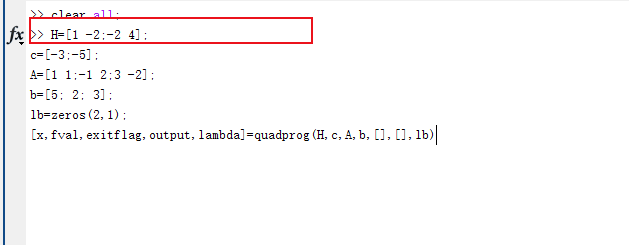
6、输入程序：>> H=[1 -2;-2 4];这是目标函数的系数

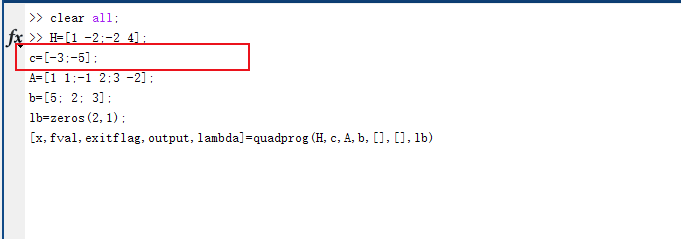
7、输入程序c=[-3;-5];这是目标函数系数

8、输入程序：A=[1 1;-1 2;3 -2];这是线性不等式约束

9、输入程序b=[5; 2; 3];>> lb=zeros(2,1);zeros功能是返回一个m×n×p×...的double类零矩阵

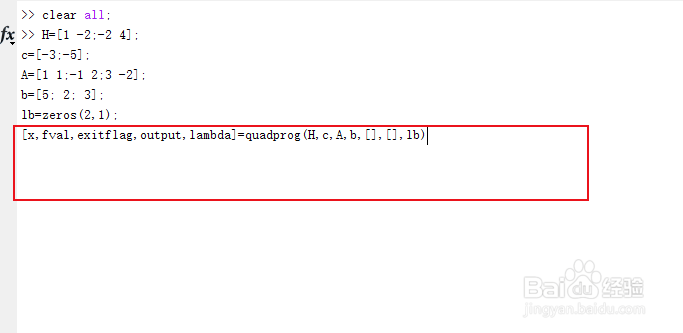
10、输入程序：>> [x,fval,exitflag,output,lambda]=quadprog(H,c,A,b,[],[],lb)记住字母书写的方式以及输入状态

11、最优解为：>> clear all;>> H=[1 -2;-2 4];c=[幻腾寂埒-3;-5];A=[1 1;-1 2;3 -2];b=[5; 2; 3];lb=zeros(2,1);[x,fval,exitflag,output,lambda]=quadprog(H,c,A,b,[],[],lb)最优解x = 2.5000 2.2500

12、最优值为>> clear all;>> H=[1 -2;-2 4];c=[-3;-5];A=[1 1;-1 2稆糨孝汶;3 -2];b=[5; 2; 3];lb=zeros(2,1);[x,fval,exitflag,output,lambda]=quadprog(H,c,A,b,[],[],lb)最优质值fval = -16.7500