【平面几何】三角形的共轭中线的由来和性质

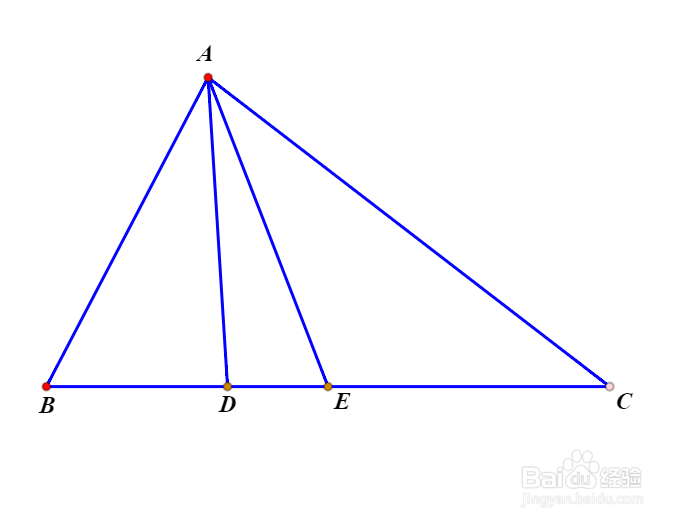
1、△ABC中，如果D是BC边上的点，E是BC中点，∠BAD=∠CAE，那么就称直线AD是△ABC经过A点的共轭中线。

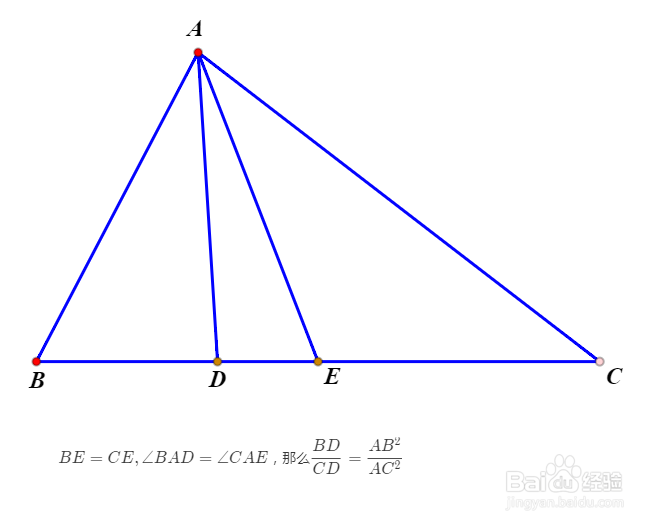
2、由此可以推出共轭中线一个等价的性质：BD/CD=(AB/AC)^2这是一个十分重要的性质。

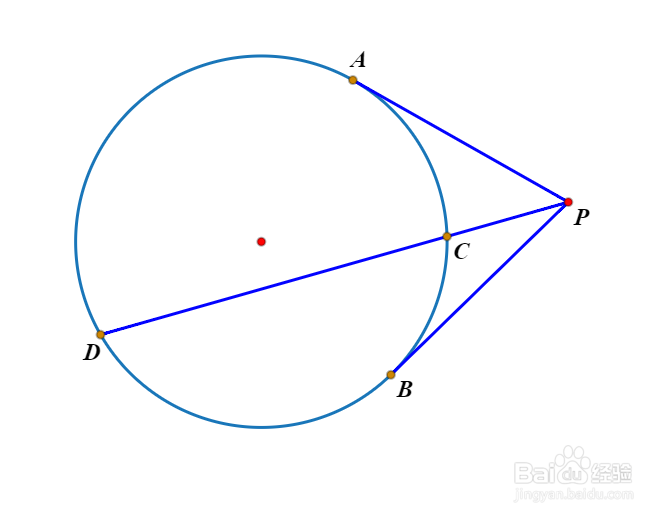
3、共轭中线出现在圆的切割线构型里面：设P是圆外一点，PA和PB是圆的切线（切点分别是A和B），PCD是圆的割线。那么PCD就是△ABC经过C点的共轭中线。这一点用面积法很容易证明。

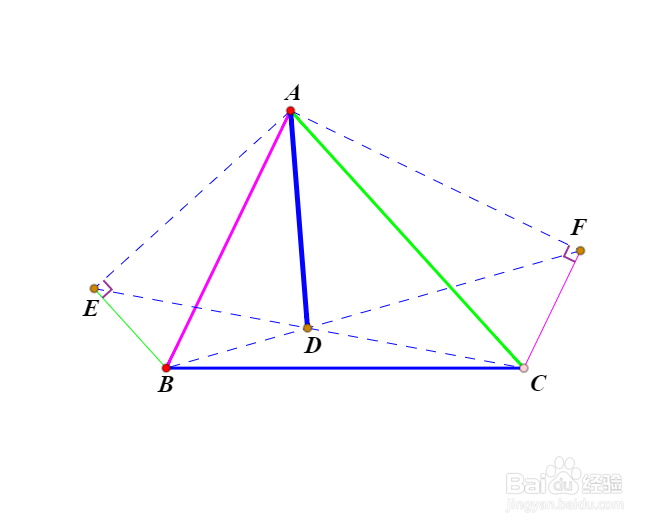
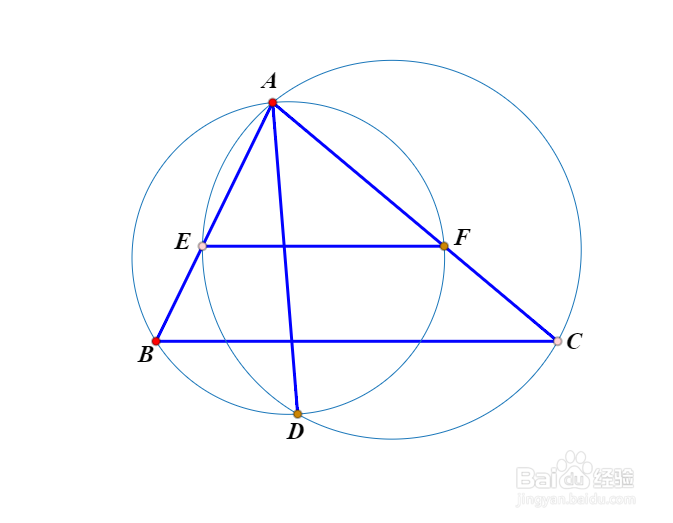
4、如下图，BE//AC，BE⊥AE，CF//AB，CF⊥AF，BF与CE交于D。那么D就是△ABC的共轭中线。

5、如下图，EF//BC，那么△ABF和△ACE的外接圆的公共弦所在直线，就是△ABC的共轭中线。

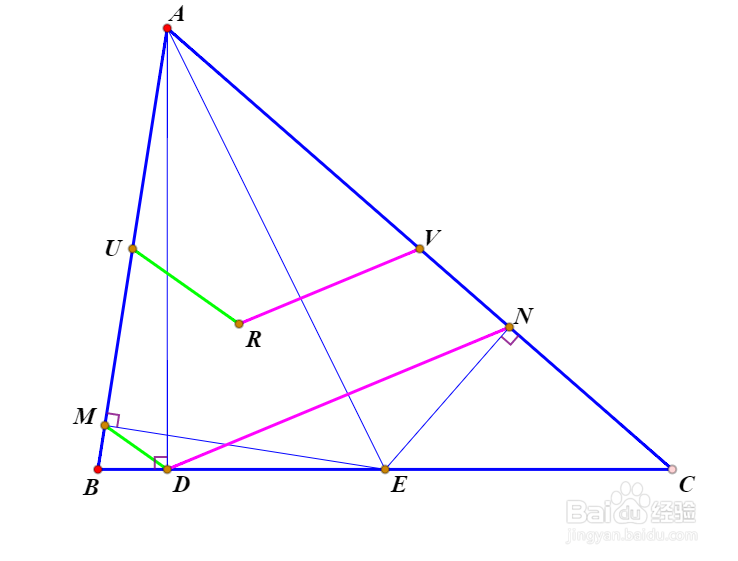
6、D是垂足，U、V、E是中点，EM⊥AB，EN⊥AC，UR//DM，VR//DN。那么AR是△ABC的共轭中线。