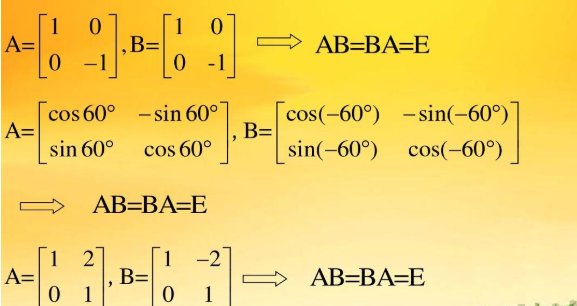ab=0矩阵能推出什么
证明:
如果AB=0,那么B的每个列都是齐次方程组AX=0的解。
设r(A)=r,那么菱诎逭幂方程组AX=0最多有n-r个线性无关的解。
所以:r(B)<=n-r=n-r(A)。
因此,r(A)+r(B)<=n。
称为n元齐次线性方程组。
设其系数矩阵为A,未知项为X,则其矩阵形式为AX=0。若设其系数矩阵经过初等行变换所化到的行阶梯形矩阵的非零行行数为r,则它的方程组的解只有以下两种类型:
当r=n时,原方程组仅有零解。
当r<n时,有无穷多个解(从而有非零解)。
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。