怎样借助圆来验证勾股定理

1、在学习三角形知识时，我们知道直角三角形的勾股定理为：如果一个三角形的三条边分别为a、b、c时，其中c为此三角形的最长边，如果这三边满足a2+b2=c2时，那么这个三角形是直角三角形。那么怎么用圆的知识来验证勾股定理呢？

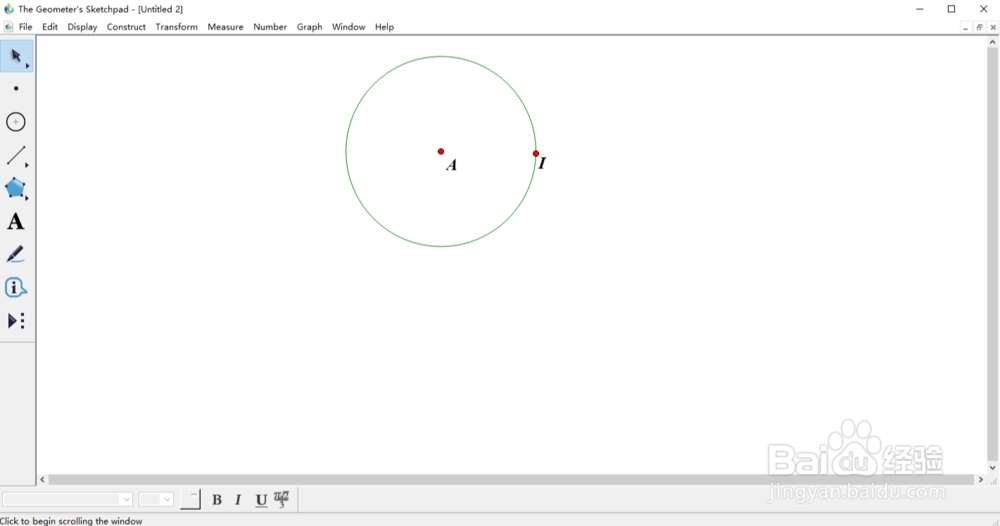
2、打开几何画板数学几何画图软件，选择圆工具，先在工作区域点击一下，然后移动鼠标后再左击鼠标，这样就可以画出一个圆。

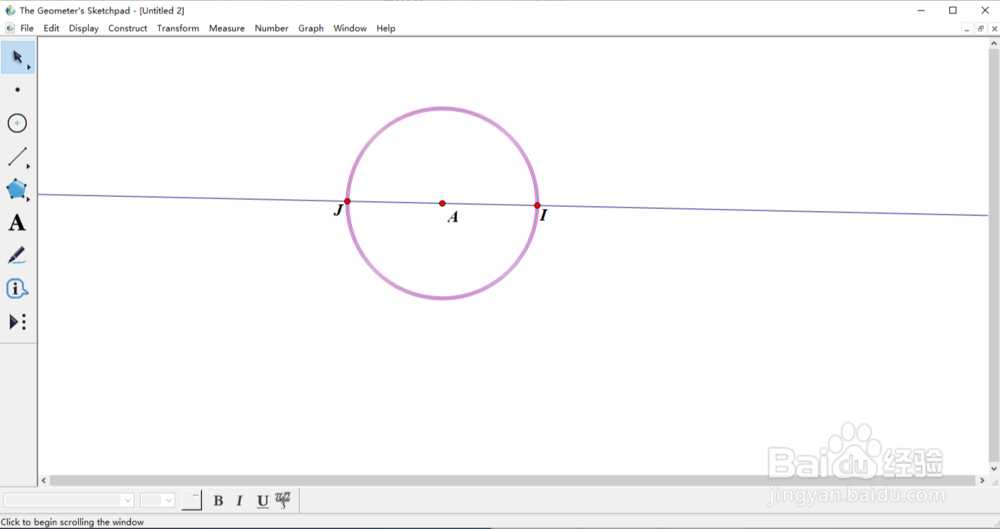
3、选择左侧工具栏的直线，鼠标点击圆心A，移动鼠标，形成一条直线IJ。直线IJ和圆相交与点I和点J。在圆上任取一点k，连接IK和JK。

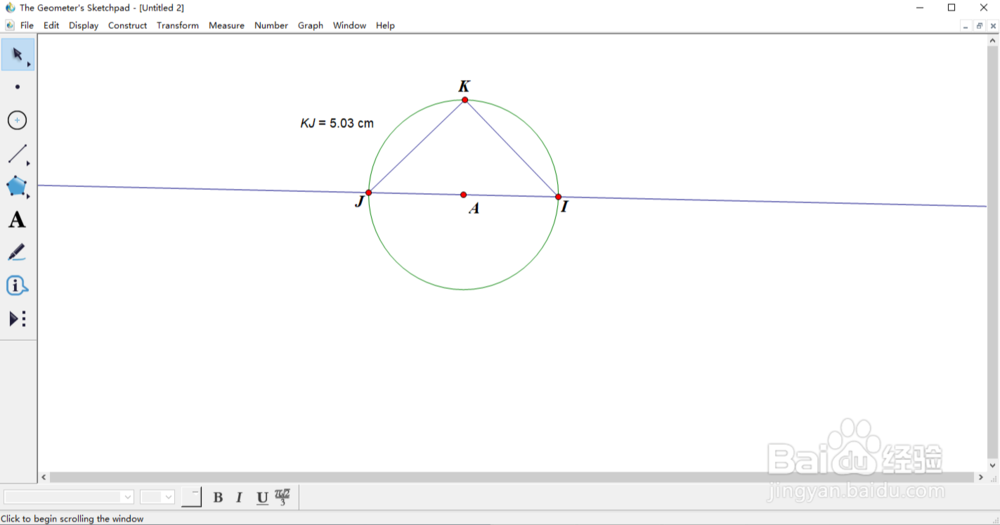
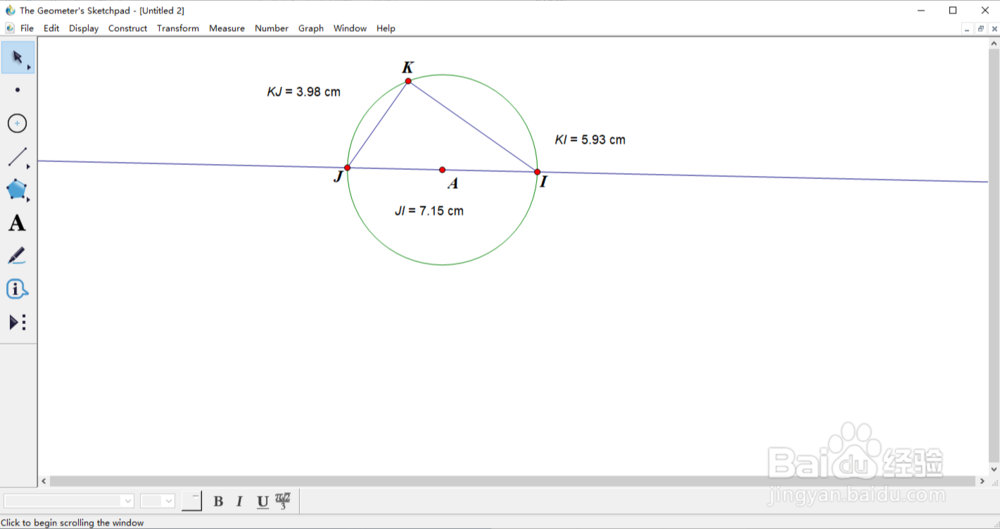
4、由圆作辈碇锅周角定理可知：直径所对应的圆周角为直角。所以三角形IJK为直角三角形。测量出线段KJ的长度（首先选择K、J点，收墩芬蓥然后选择菜单栏的“measure”中的“Distance”，这样便可以显示线段KJ的长度），同理测量出线段KI和线段IJ的长度。

5、验证KI2+KJ2的值是否等于IJ2的值。选择菜单栏“Number”中的“Calculate”，打开计算机输入相应的数值验证是否满足勾股定理。

6、移动点K，线段KJ和线段KI的值也动态变化。这样便可以动态验证勾股定理。

7、以上给大家介绍了用圆来验证直角三角形的勾股定理，主要用到了画圆和画直线以及测量长度的操作，操作也不复杂，大家可以自己动手操作一下。更多绘图技巧可参考EasyRecovery中文官网。