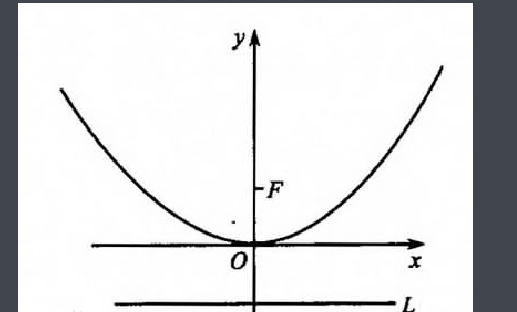
抛物线方程

抛物线方程是指抛物线的轨迹方程，是一种用方程来表示抛物线的方法 。在几何平面上可以根据抛物线的方程画出抛物线。抛物线在合适的坐标变换下，也可看成二次函数图像。

抛物线表达式：y=ax²+bx+c（a≠0）的顶点坐标公式是（-b/2a，（4ac-b²）/4a) y=ax²+bx的顶点坐标是（-b/2a，-b²/4a)。

抛物线定义

平面内与一个定点F和一条直线l的距离相等的点的轨迹叫做抛物线，点F叫做抛物线的焦点，直线l叫做抛物线的准线，定点F不在定直线上。它与椭圆、双曲线的第二定义相仿，仅比值（离心率e）不同，当e=1时为抛物线，当0<e<1时为椭圆，当e>1时为双曲线。

一般式y=ax²+bx+c（a≠0）。提出a得y=a(x²+b/a x)+c。

配方得y=a(x+b/2a)²+(4ac-b²)/4a。令平方项为0 x=-b/2a y=(4ac-b²)/4a。

所以顶点坐标为 ﹛-b/2a,(4ac-b²)/4a﹜。