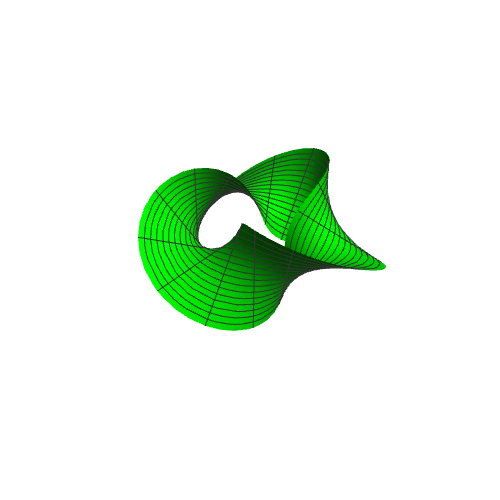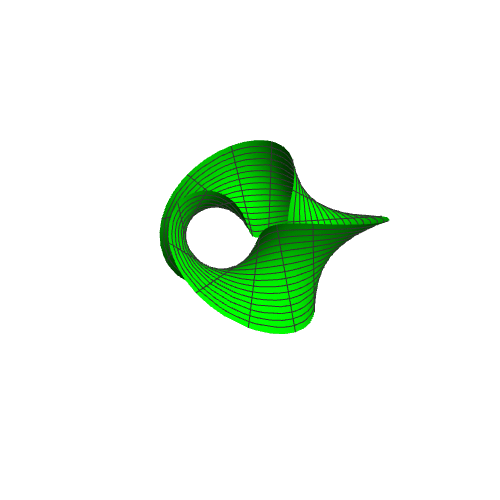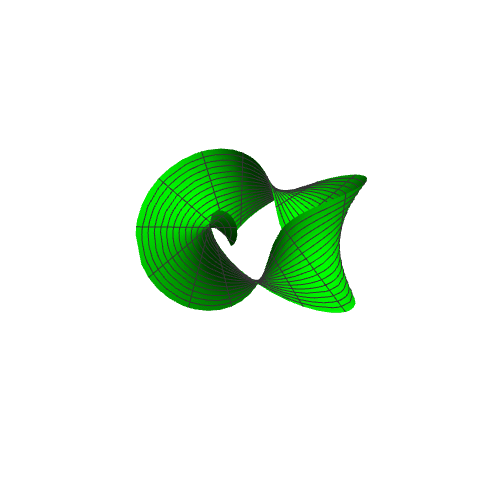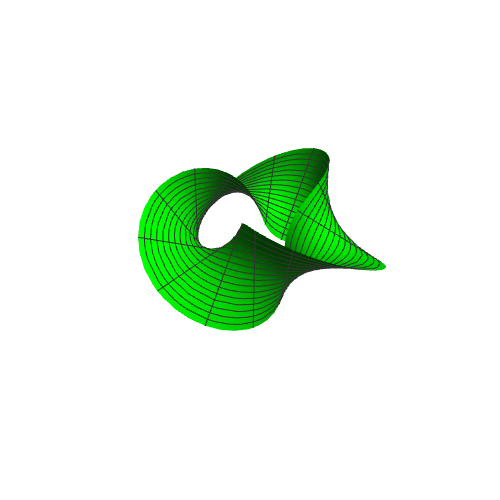用Mathematica画一个翻卷的莫比乌斯带

1、以 {3 Cos[u], 3 Sin[u], 0} 为圆心、{-3 Sin[u], 3 Cos[u], 0} 为法线、半径为2的圆的参数方程是：{Cos[u] (3 + 2 Cos[u - v]), (3 + 2 Cos[u - v]) Sin[u], 2 Sin[u - v]}这其实是一个圆环。

2、令v=3*u/2，就可以画出某条莫比乌斯带的边界线：{(3 + 2 Cos[u/2]) Cos[u], (3 + 2 Cos[u/2]) Sin[u], -2 Sin[u/2]}u的取值范围是0到2*pi。

3、莫比乌斯带的参数方程是：{(3 + (-2 + 4 t) Cos[u/2]) Cos[u], (3 + (-2 + 4 t) Cos[u/2]) Sin[u],2 (1 - 2 t) Sin[u/2]}其中，u从0到2*Pi，t从0到1。

4、而：{(3 + (-2 + 4 t) Cos[n + u/2]) Cos[u], (3 + (-2 + 4 t) Cos[n + u/2]) Sin[u], 2 烫喇霰嘴(1 - 2 t) Sin[n + u/2]}随着n从1递增到2*Pi，表现出来的，就是一条翻卷的莫比乌斯带。

5、上面的是一扭莫比乌斯带，下面的参数方程则是三扭莫比乌斯带：{Cos[u] (3 + (-2 + 4 t) Cos[(3 u)/2]),(3 + (-2 + 4 t) Cos[(3 u)/2]) Sin[u],2 (1 - 2 t) Sin[(3 u)/2]}

6、翻卷的三扭莫比乌斯带：{Cos[u] (3 + (-2 + 4 t) Cos[n + (3 u)/2]),(3 + (-2 + 4 t) Cos[n + (3 u)/2]) Sin[u],2 (1 - 2 t) Sin[n + (3 u)/2]}