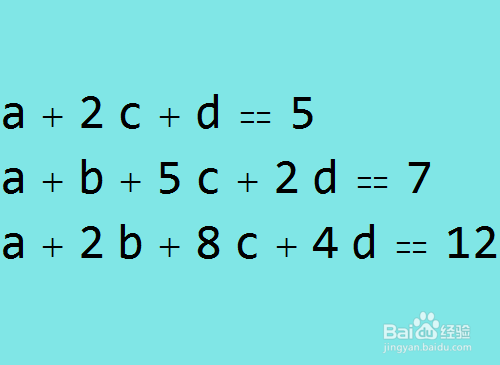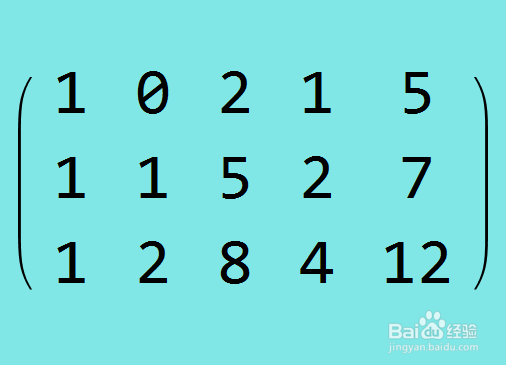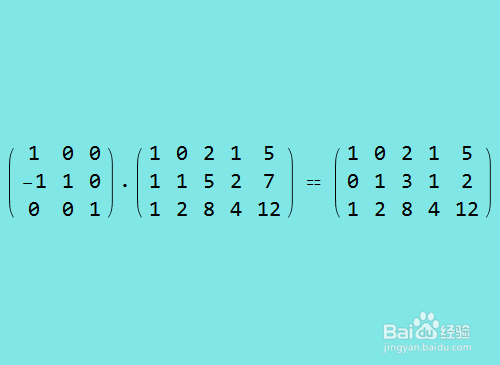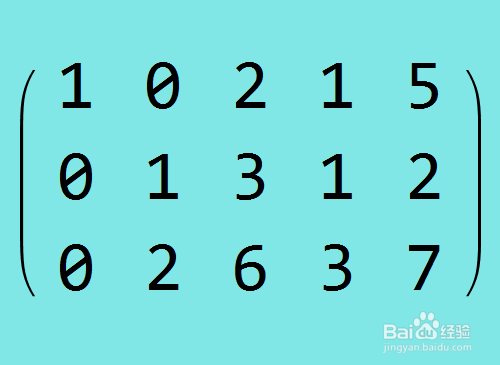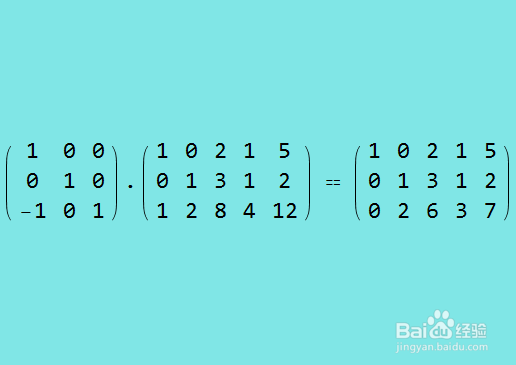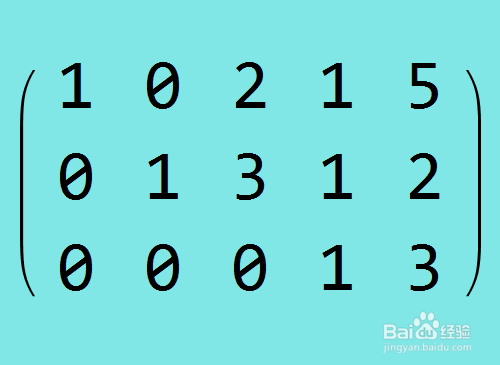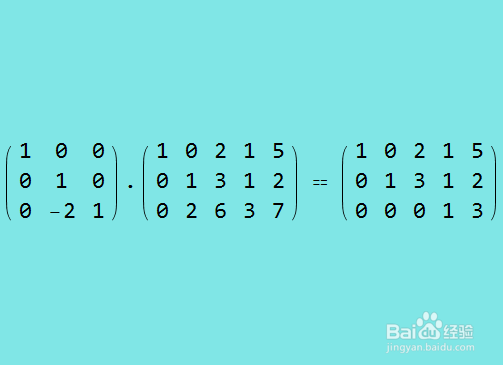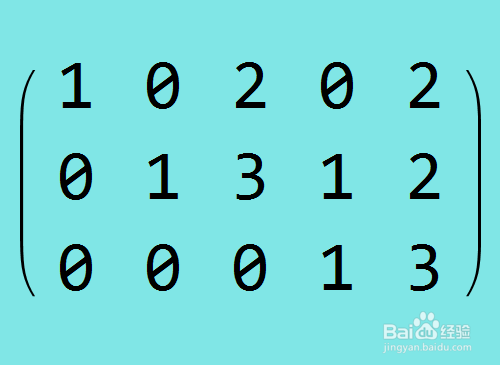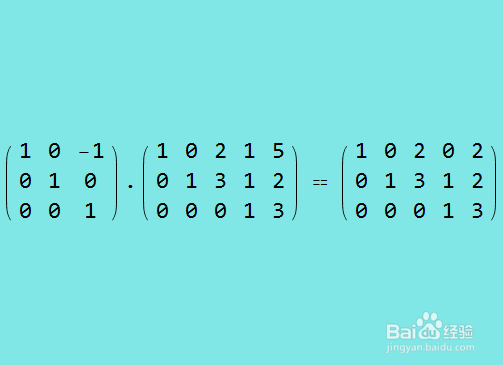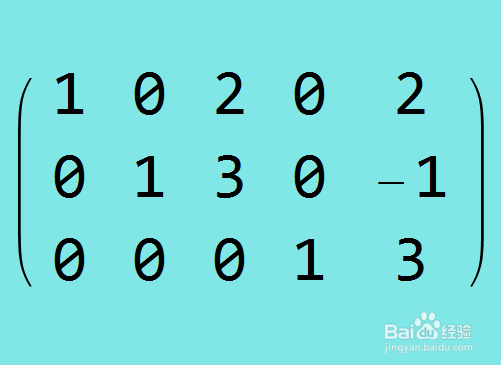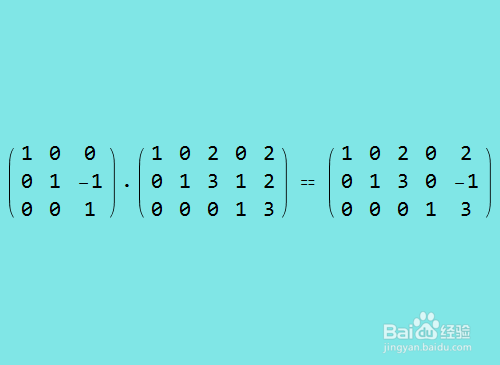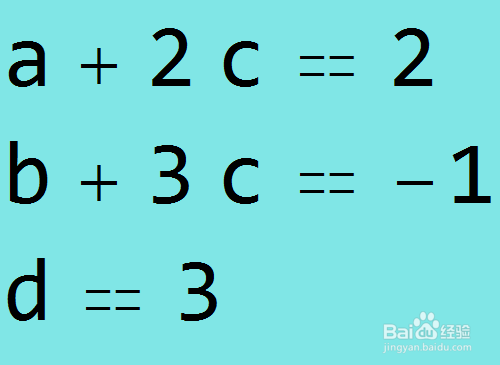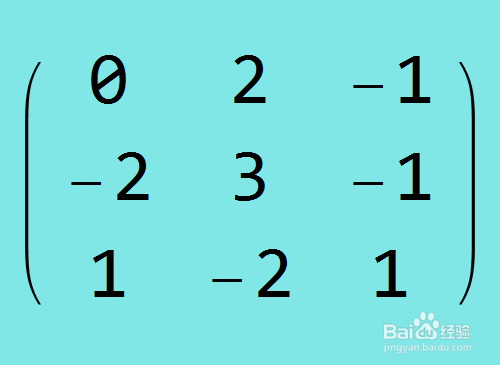【抽象代数】怎么用初等矩阵实现行约简

1、书中的例子，是解一个方程组。如下图所示，未知数是a、b、c、d。这是一个不定方程组。

2、提取系数矩阵，并把等号右边的数字，作为常数项的系数，放在矩阵最后一列。系数矩阵如下：j = {{1, 0, 2, 1, 5魈胺闹臣}, {1, 1, 5, 2, 7}, {1, 2, 8, 4, 12}};

3、行约简第一步，把第一行乘以-1，加到第二行上，结果如下图：j[[2]] = j[[2]] 颍骈城茇- j[[1]];

4、步骤3的行约简，可以用矩阵乘法实现。观察下图，左边矩阵是一个3阶初等矩阵。

5、行约简第二步，把第一行乘以-1，加到第三行上，这也可以用初等矩阵的乘法来实现。

6、行约简第三步，把第二行乘以-1，加到第三行上。

7、行约简第四步，把第三行乘以-1，加到第一行上。

8、行约简第五步，把第三行乘以-1，加到第二行上。

9、把矩阵再转化为方程组，发现方程组简单多了。这仍旧是不定方程组，解完全一样。

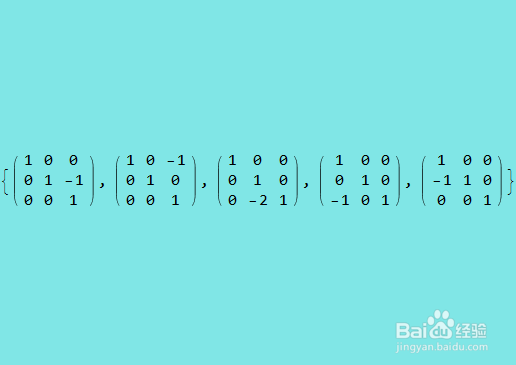
10、五部行约简，用到了五个初等矩阵，按顺序从右往左排列：

11、这五个初等矩阵的乘积是：

12、一步到位的行约简过程：