如何证明三角形内角和为180度

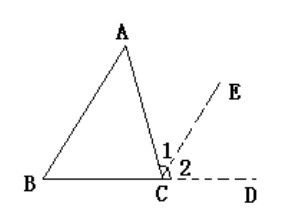
1、证 法 一 ： 作 BC 的 延 长 线 CD ， 过 点 C 作 CE∥BA ， 则 ∠1=∠A ， ∠2=∠B ， 又 ∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°

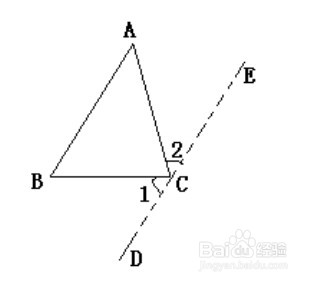
2、证 法 二 ： 过 点 C 作 DE∥AB ， 则 ∠1=∠B ， ∠2=∠A ， ∵∠1+∠ACB+∠2=180°∴∠A+∠ACB+∠B=180°

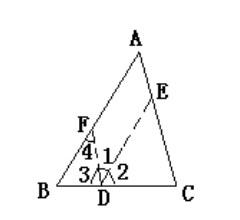
3、证 法 三 ： 在 BC 上 任 取 一 点 D ， 作 DE∥BA 交 AC 于 E ， DF∥CA 交 AB 于 F ， 则 有 ∠2=∠B ， ∠3=∠C,鹳帕鄯区∠1=∠4,∠4=∠A。∴∠1=∠A。又∵∠1+∠2+∠3=180°∴∠A+∠B+∠C=180°