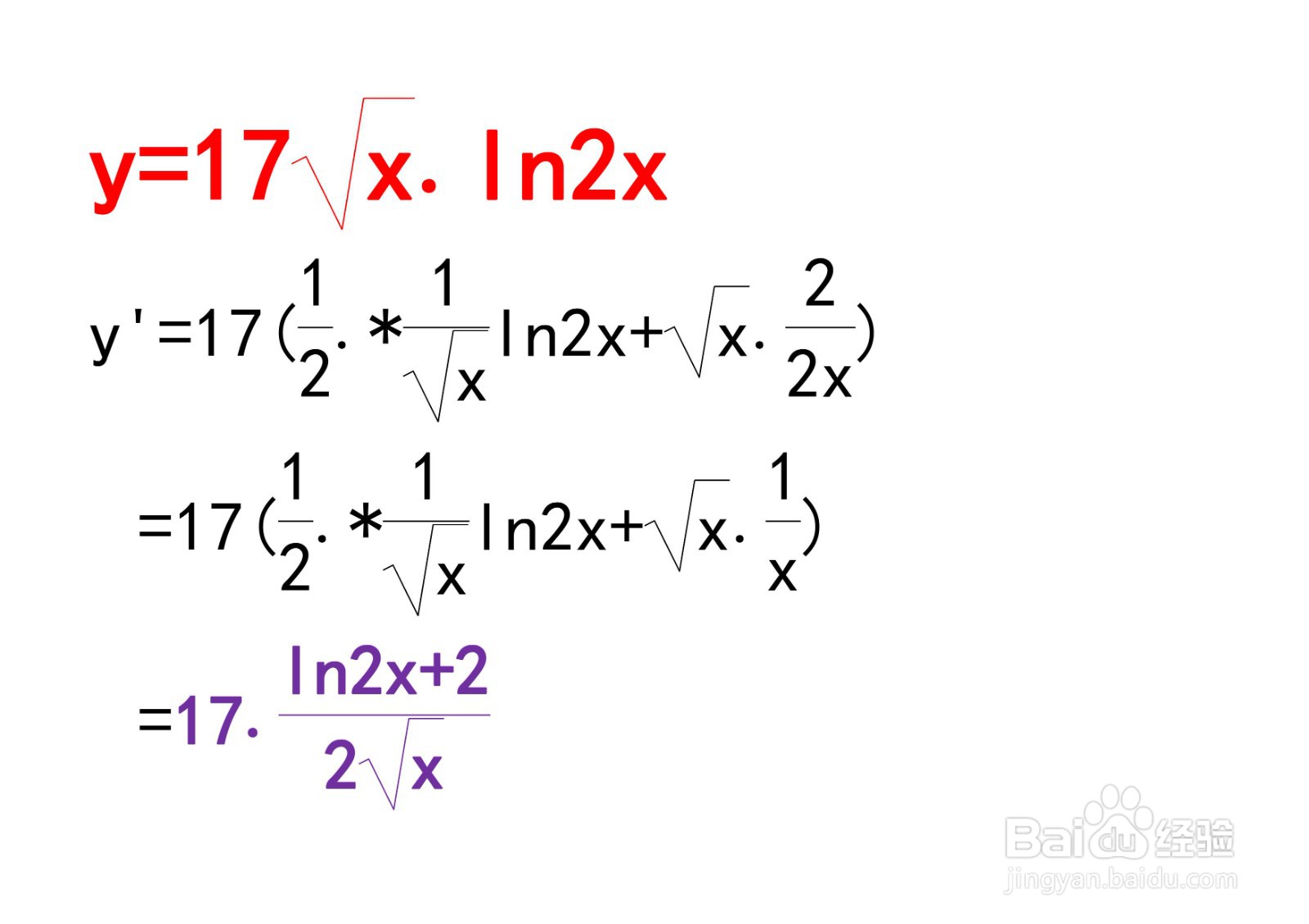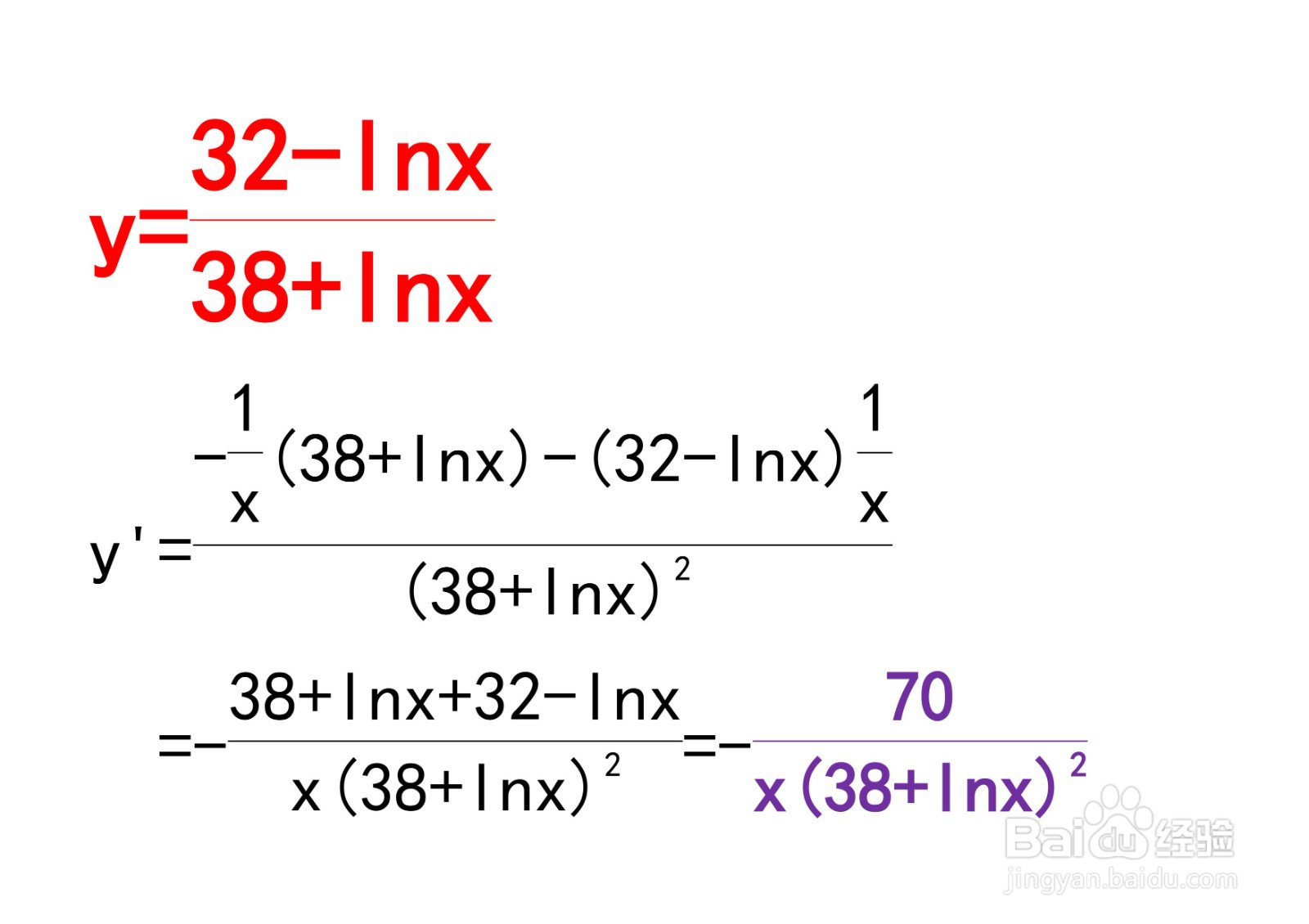函数的一阶导数练习题及详细解析A7

本文通过幂函数、对数函数、三角函数的导数公式等，以及函数和差、乘积、商的求导法则，以10个函数求导为例详细介绍计算步骤过程。

※.幂函数的求导

1、例题:计算y=(243x-295)^(-1/2)导数思路：幂函数的求导公式应用：dy/dx=(-1/2)*(243x-295)^(-3/2)*243.

2、例题:函数y=(46-8x+17x³)7 导数计算步骤思路：幂函数的链式求导法则，具体过程为：y'=7*(46-8x+17x³)6 *(46-8x+17x³)'=7*(46-8x+17x³)6 *(-8+3*17x2).

3、例题:函数y=√(1+8x2)的导数计算因为：y=(1+8x2)^(1/2),进一步由幂函数求导公式有：所以：y'=(1/2)*(1+8x2)^(-1/2)*2*8x=8x*(1+8x2)^(-1/2).

※.对数函数求导

1、例题:计算y=ln(152x²+291) 导数 思路：由对数的导数计算公式，求解函数的导数，即：dy/dx=(152x²+291)'/(152x²+291)=304x/(152x²+291).

2、例题:计算y=17√x.盟敢势袂ln2x 的导数 思路：本题是幂函数和对数函数的乘积，用到函数乘积的求导法则以及幂函数和对数函数的嫫绑臾潜求导，步骤为：y'=17[1/2.ln2x*(1/√x )+√x(2/2x)]=17(1/2.ln2x*(1/√x )+1/√x]=17*(ln2x+2)/(2√x) 。

3、例题:计算y=(32-l艘绒庳焰nx)/(38+lnx)的导数思路：本题是对数函数商的求导法则的应用，详细过程如下：y'=[-1/x*(38+lnx)-(32-lnx)*(1/x)]/(38+lnx)²=-1/x*[(38+lnx)+(32-lnx)]/(38+lnx)²=-70/[x(38+lnx)²].

※.三角函数求导

1、例题:函数y=cos(46-20x)导数计算步骤思路：本题是正弦函数和一次函数的复合函数，主体为余弦函数，使用链式求导即可，过程如下：y'=-sin(46-20x)(46-20x)' =20sin(46-20x)。

2、例题:函数y=7sinx-cos5x的导数计算思路：本题是正弦函数和余弦函数的和差函数，由和差函数的导数及三角函数的求导公式，即可计算，详细步骤如下。y'=7cosx+sin5x.5=7cosx+5sin5x。

3、例题:函数y=sin2x6的导数计算思路：本题是正弦函数与幂函数的复合函数，使用复合函数求导法则及正弦函数的导数公式计算即可。y'=cos(2x^6)*(2x^6)'=2*6x^5*cos(2x^6)=12*x^5*cos(2x^6)。

※.多个函数乘积求导

1、例题:函数y=xsin5垓矗梅吒x.ln4x的导数计算思路：本题是幂函数、三角函数和对数函数的乘积，仍需使用函数乘积求导法则及相关函数的导数公式计算一阶导剞麽苍足数。y'=sin5x.ln4x+x(5cos5xln4x+sin5x/x)=sin5x.ln4x+sin5x+5xcos5x*ln4