因式分解12种方法（一）

1、提公因法如果一个多项式的各项都含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式。例1、分解因式x3-2x2-x(2003淮安市中考题)x3-2x2-x=x(x2-2x-1)

2、应用公式法由于分解因式与整式乘法有着互逆的关系，如果把乘法公式反过来，那么就可以用来把某些多项式分解因式。例2、分解因式a2+4ab+4b2(2003南通市中考题)解：a2+4ab+4b2=（a+2b）2

3、 3、分组分解法要把多项式am+an+bm+bn分解因式，可以先把毋队末哎它前两项分成一组，并提出公因式a，把它后两项分成一组，并提出公因式b，从而得到a(m+n)+b(m+n),又可以提出公因式m+n，从而得到(a+b)(m+n)例3、分解因式m2+5n-mn-5m解：m2+5n-mn-5m=m2-5m-mn+5n=(m2-5m)+(-mn+5n)=m(m-5)-n(m-5)=(m-5)(m-n)

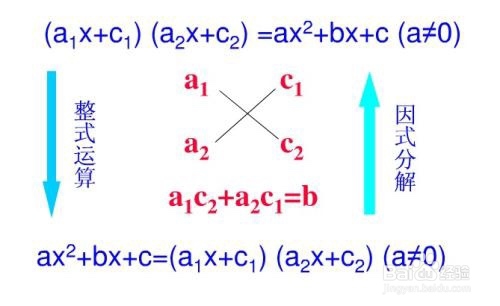
4、十字相乘法对于mx2+px+q形式的多项式，如果a×b=m,c×d=q且ac+bd=p，则多项式可因式分解为(ax+d）(bx+c)例4、分解因式7x2-19x-6分析：1×7=7,2×(-3)=-61×2+7×(-3)=-19解：7x2-19x-6=（7x+2）(x-3)

5、配方法对于那些不能利用公式法的多项式，有的可以利用将其配成一个完全平方式，然后再利用平方差公式，就能将其因式分解。例5、分解因式x2+6x-40解x2+6x-40=x2+6x+(9)-(9)-40=(x+3)2-(7)2=[(x+3)+7]*[(x+3)–7]=(x+10)(x-4)

6、拆、添项法可以把多项式拆成若干部分，再用进行因式分解。例6、分解因式bc(b+c)+ca(c-a)-ab(a+b)解：bc(b+c)+ca(c-a)-ab(锾攒揉敫a+b)=bc(c-a+a+b)+ca(c-a)-ab(a+b)=bc(c-a)+ca(c-a)+bc(a+b)-ab(a+b)=c(c-a)(b+a)+b(a+b)(c-a)=(c+b)(c-a)(a+b)