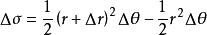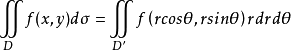请问极坐标下的累次积分怎么转化为直角坐标下的累次积分

计算二重积分的基本思锭缠愁颊路是将其化作累次积分(也即两次定积分)，要把二重积分化为累次积分，有两个主要的方式：一是直接使用直角坐标，二是使用极坐标。这是计算二重积分的两个主要的武器。

二重积分是二元函数在空间上的积分，同定积分类似，是某种特定形式的和的极限。本质是求曲顶柱体体积。重积分有着广泛的应用，可以用来计算曲面的面积，平面薄片重心等。平面区域的二重积分可以推广为在高维空间中的（有向）曲面上进行积分，称为曲面积分。

扩展资料：

在极坐标系下计算二重积分，需将被积函数f（x，y），积分区域D以及面积元素dσ都用极坐标表示。函数f（x，y）的极坐标形式为f（rcosθ，rsinθ）。为得到极坐标下的面积元素dσ的转换，用坐标曲线网去分割D，即用以r=a，即O为圆心r为半径的圆和以θ=b，O为起点的射线去无穷分割D，设Δσ就是r到r+dr和从θ到θ+dθ的小区域，其面积为

，可得到二重积分在极坐标下的表达式：

参考资料来源：百度百科-二重积分