燕尾模型在小学数学几何题中的应用

1、利用燕尾模型解决问题，重点是找到燕尾。找燕尾在实际中有两个办法，第一是找到题目中已知比例的边和边所对应的那个点形成燕尾；第二个是如果找不到对应的那个点形成两个三角形，那就要画辅助线形成燕尾。后面会结合具体题目详细讲解第一个办法。

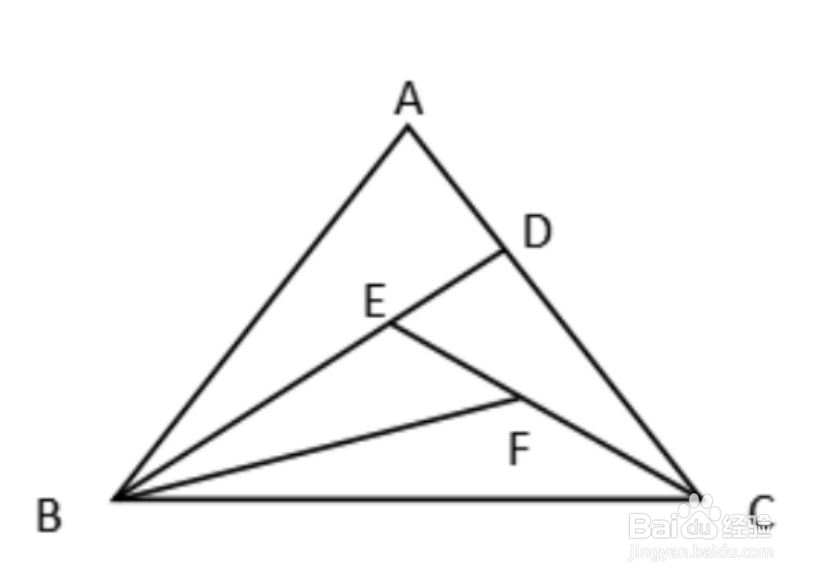
2、如图所示，若△ABC的面积是60，AD砜实蛰斓:DC=1:3,BE:ED=4:1,EF:FC=4:5,则△BEF的面积是多少？器皆阄诟分析：从图形可知，我们不知道BEF的边和高，也无法直接求出边和高，所以不能直接利用三角形的面积公式求解，可以看出BEF是ABC里的一部分，而三角形ABC的面积是已知的，所以只要求出BEF和ABC的比例关系，就可以知道BEF的面积了。那么我们先看下题目中另一个已知条件，就是一条边中两部分的比例关系，这个时候就可以利用燕尾模型解题了。步骤： 1. AD:DC=1:3，那么找到AC对应的点B，这样就形成了燕尾BAD和BCD，那么：S△BAD:S△BCD=AD:DC=1:3,也就是S△BCD=3/4S△ABC 2.BE:ED=4:1，那么找到BD对应的点C，这样就形成了燕尾CBE和CDE，那么：S△CBE:S△CDE=BE:ED=4:1,也就是S△CBE=4/5S△BCD 3.EF:FC=4:5,那么找到CE对应的点B，这样就形成了燕尾BEF和BFC，那么：S△BEF:S△BFC=EF:FC=4:5,也就是S△BEF=4/9S△CBE 所以：S△BEF=4/9*4/5*3/4*S△ABC=4/15*60=16