函数y=a/(6x^2-2)的图像规律

本经验通过函数的定义域、图像性质、渐近线等，以及a值的不同对函数性质的影响来介绍函数y=a/(6x^2-2)的图像规律，其中a=1,2,3,4,5,6.

工具/原料

函数性质及图像有关知识

导数有关知识

1.不同a值情况下的函数图像

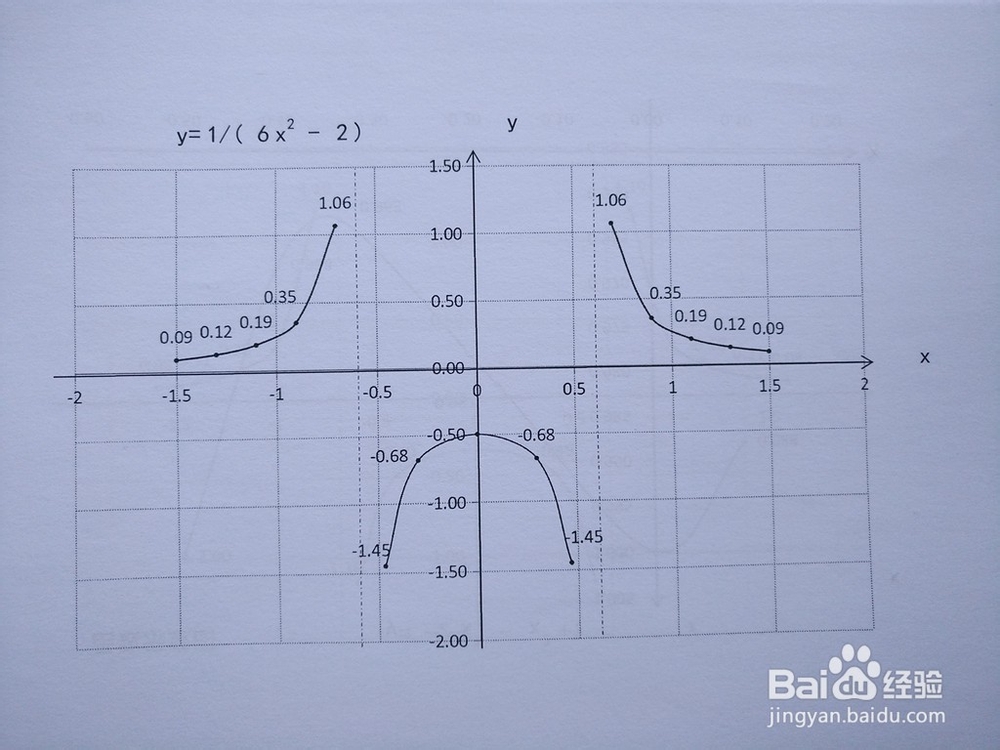
1、函数y=1/(6x^2-2)的图像。

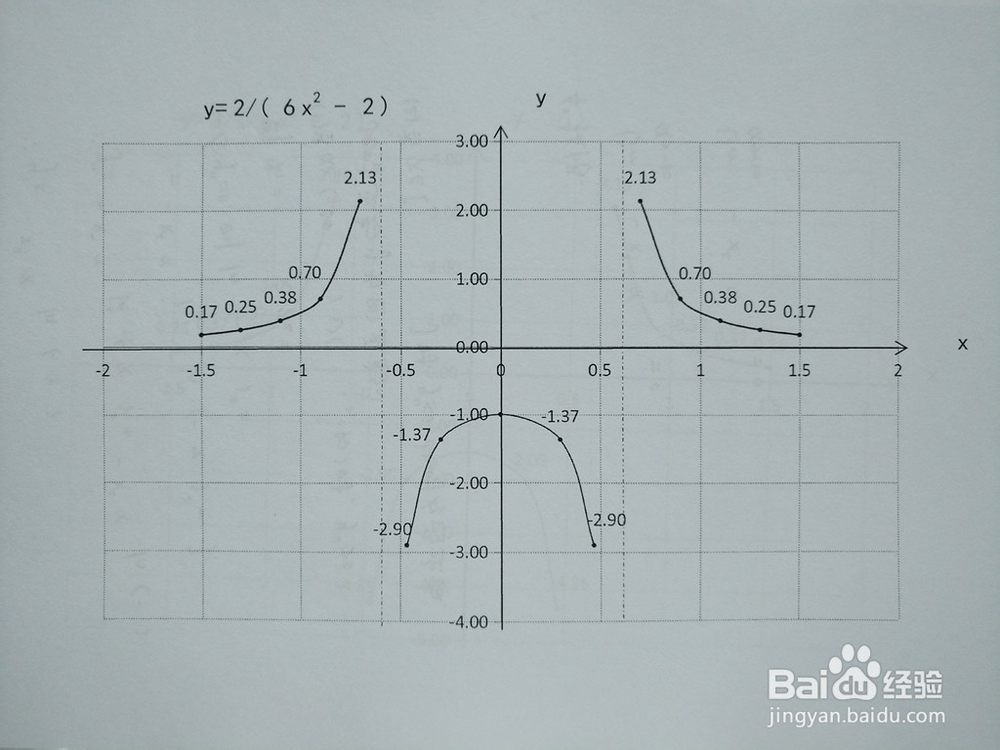
2、函数y=2/(6x^2-2)的图像。

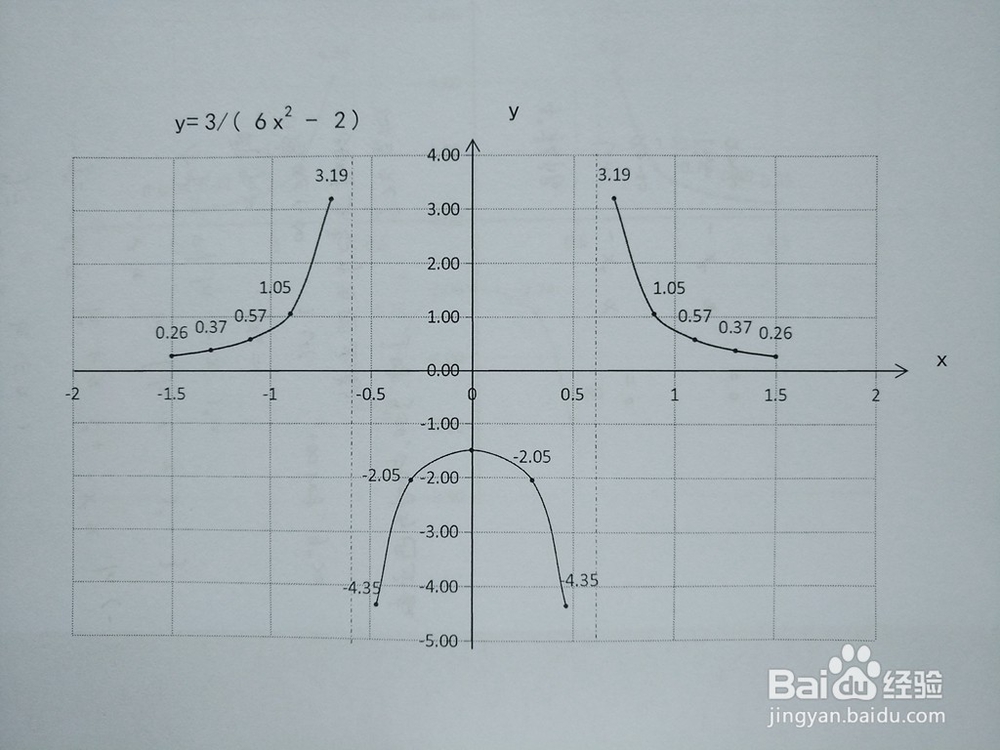
3、函数y=3/(6x^2-2)的图像。

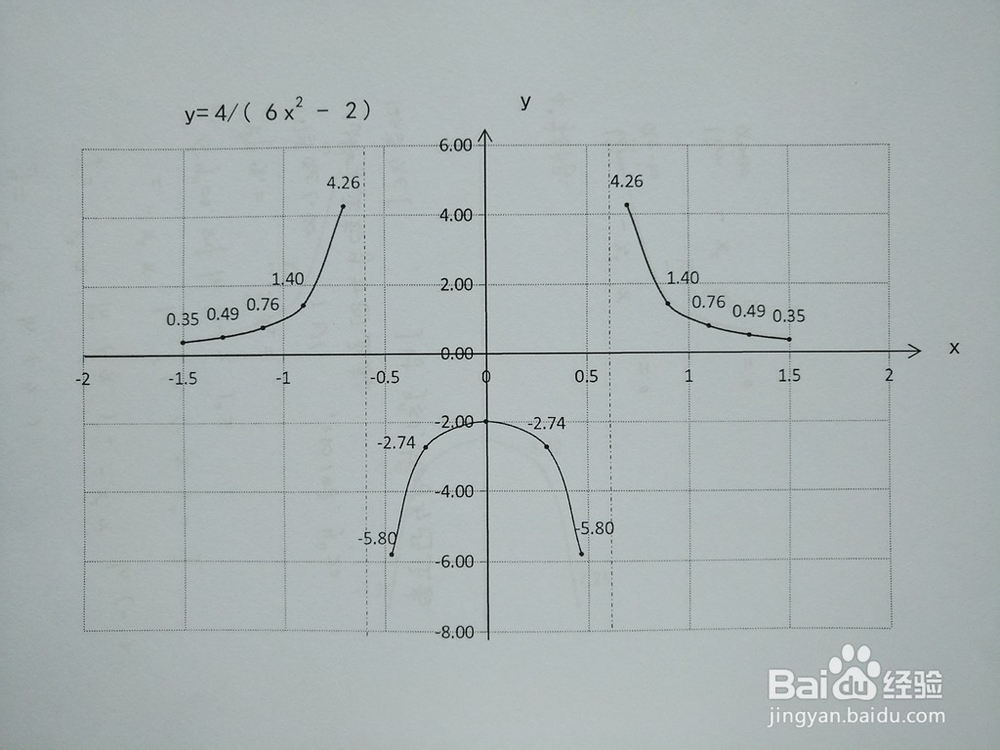
4、函数y=4/(6x^2-2)的图像。

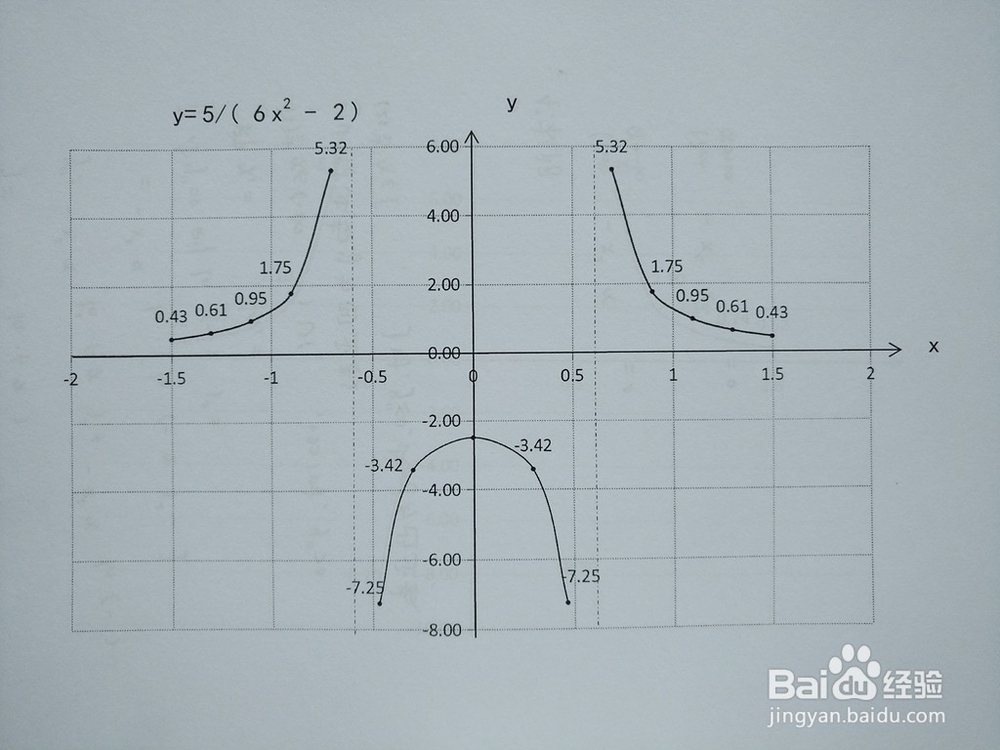
5、函数y=5/(6x^2-2)的图像。

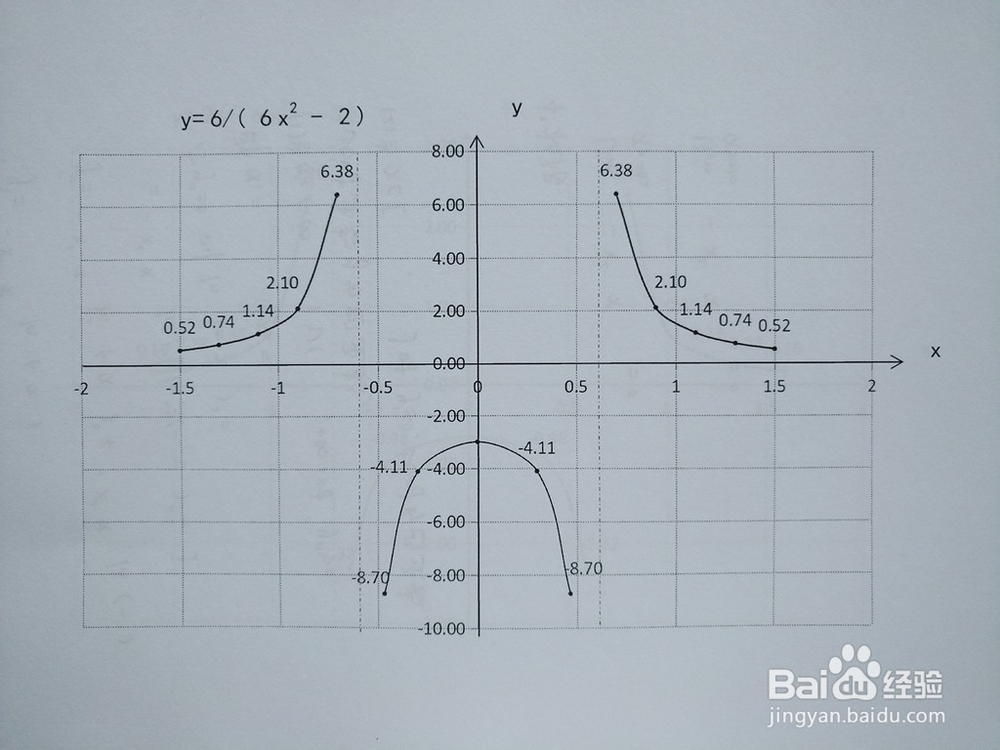
6、函数y=6/(6x^2-2)的图像。

二、函数性质归纳

1、函数y=a/(6x^2-2)的图像规律,其中a=1-6。 1.从定义域上看，分母不为零，则x^2≠1/3,由此判断以上情形函数均有两条垂直渐近线，分别为x1=-√3/3，x2=√3/3. 2.从图像上看，以两条垂直渐近线为界，函数图像分布在三个区间段中，即（-∞，-√3/3）、（-√3/3，+√3/3）、（+√3/3，+∞）上。

2、 3.从单调性上看，由于y’=-3ax/(3x^2-1)^2,其中a>0,所以函数单调性取决于x的正负，注意前面有负号，则x为正则为减函数，为负则为增函数。 4.从凸凹性上看，y媪青怍牙"=3a(9x^2+1)/(3x^2-1)^3 ，由于分子大于0，可见函数的凸凹性取决分母的正负，即取决于3x^2-1整体的正负。即当整体为正，则为凹函数，反之为凹函数。

3、 5.a值大小对函数性质的影响（1）在函数一次导数中，y’=-3ax/(3x^2-1)^2,当自变匪犬挚驰量x不变，a增大时，y’减小，即在x相同处函数图像的切斜的斜率越小，切线越倾向平行于x轴或重合。（2）在函数二次导数中，y"=3a(9x^2+1)/(3x^2-1)^3，当自变量x不变，a增大时，y"增大，即在x相同处，函数凸得或凹得趋势更快。