网络画板应用——Malfatti正方形问题进一步探索

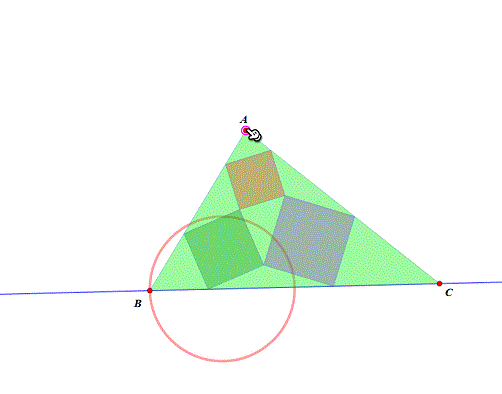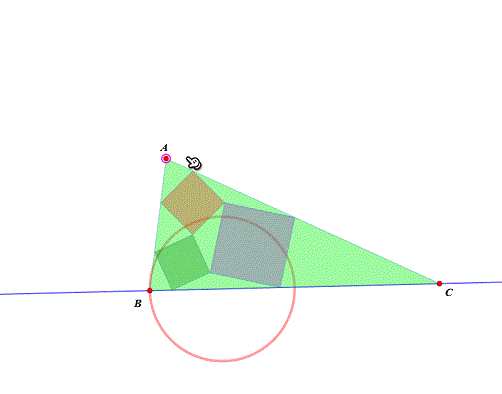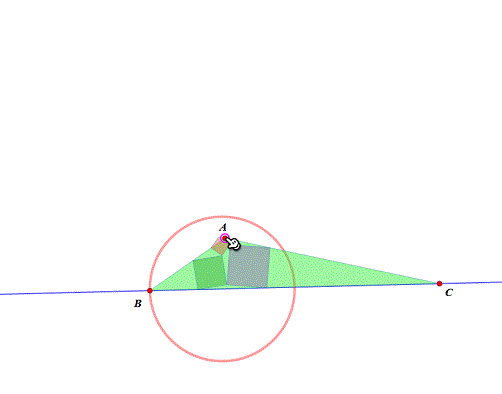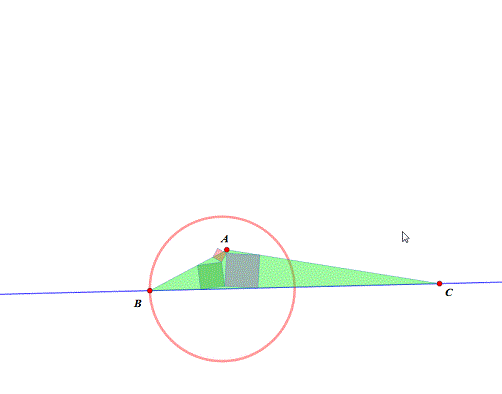
最近几天，在回顾以前写的《Malfatti正方形的尺规作图法》里面的问题的时候，发现了一个严重的错误。当我们移动A的位置的时候，会发现△ABC的内接正方形有可能会跑出三角形。这是怎么回事呢？ 在用网络画板做了几个实验之后，终于搞明白状况了。原来，这个构造存在一些“禁区”！

工具/原料

电脑+互联网

网络画板

准备

1、 这个图的作图步骤，与《Malfatti正方形的尺规作图法》里面的步骤是一致的。所以，这里不做多余的介绍！ 提一点，在作图的时候，我构造了一个▲，要求：▲的三条中线，分别与△ABC的三条高的方向相同。

2、 所以，当△ABC的内接正方形跑出三角形的时候，▲也肯定出错了。 于是我们可以通过界定▲的形状，来逆向界定△ABC的形状。在这之前，我们很容易验证，当△ABC是锐角三角形的时候，是存在Malfatti正方形的构造的！所以，我们现在规定，∠A是钝角。 字母可能有所出入，大家看的时候，尽量就题论题。参考《网络画板晋阶——解决几何问题一则》。在这篇文章里面，所说的△ABC不是本文的△ABC，而是▲！ 以此为基础，我们来搞定本文一开始的问题。

正题

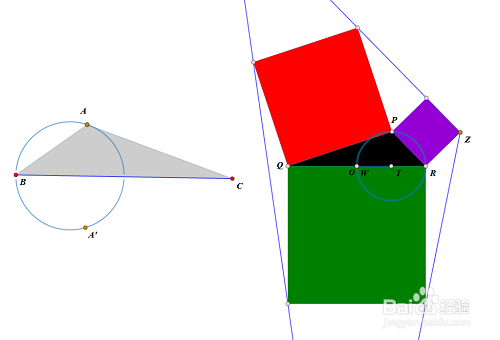
1、 固定两个点Q、R，RQ中点为O，RO中点为T，W为线段OT上的动点，以TW为半径作圆T，P为圆T上的动点。那么，△PQR就是上面提到的▲； 从△PQR的三条边出发，向外作三个正方形，然后再构造出△XYZ。如下图，至于具体的步骤，请到网络画板官网搜索《Malfatti测试2》。

2、 在平面上固定两个点C、B，构造△ABC，使得△ABC与△ZX孢亨槐溲Y相似（具体的构造方法，请大家自己思考，或者参考《Malfatti测试2》）； 依次选择点P，点A，构造轨迹（此暄跬烷记为Ω），可以发现，A的轨迹Ω应该是个圆（由于我的水平不足，只能构造出半圆，另外那个半圆是A关于BC的对称点的轨迹（为什么轨迹不能直接作对称变换呢），请教大家，怎么能够使得A的轨迹Ω是一个完整的圆呢？不过，对于解决问题影响不大）； 依次选择点W、轨迹Ω，构造Ω的轨迹，可以发现Ω的轨迹应该是个圆盘（同样的，我只能得到半个圆盘）。这个圆盘内部的点，与B、C组成的三角形不可能构造出Malfatti正方形。

3、 这一步，另起炉灶，参考《Malfatti测试3》。 固定B、C两点，BC中点为U，UC中点为V，以VC为半径作圆V，A是圆V上动点。可以知道，如果A位于圆V的内部，△ABC不存在Malfatti正方形的构造。 试试“附着-脱离”功能，不会用的话，看这里——《对网络画板“附着/脱离”功能的初步探索》。

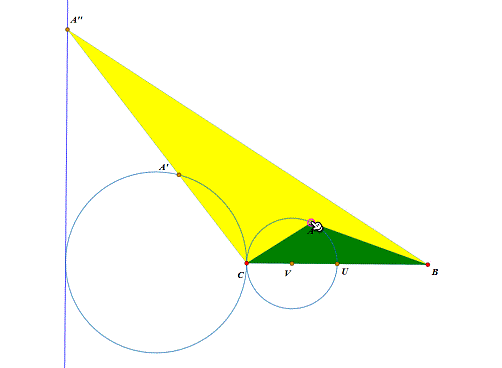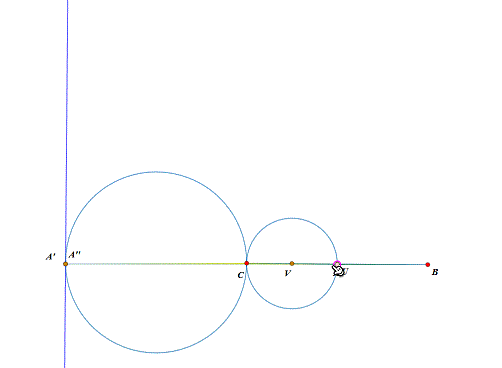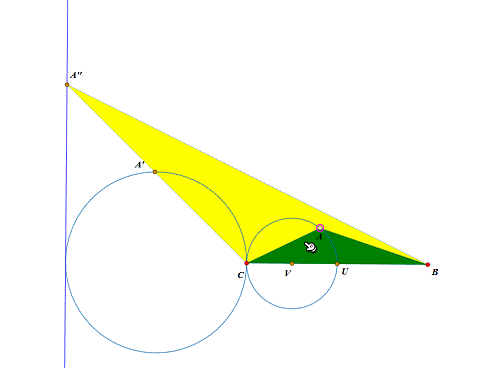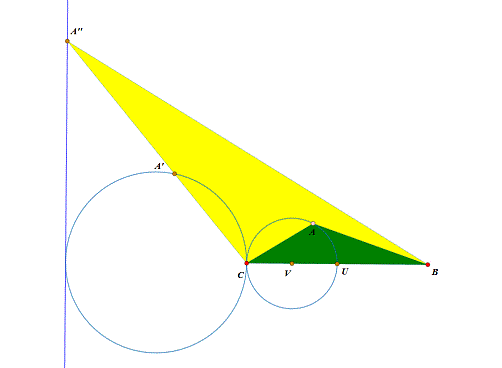
4、 如果放开∠A为钝角的限制呢？仍旧参考《Malfatti测试3段乒错烊》。 我们假设∠C为锐角，那么，构造△A'潮贾篡绐CB，使得△A'CB与△CAB相似，依次选择A、A'，构造A'的轨迹，发现也是一个圆。这个圆其实可以通过缩放得到，以B为缩放中心，缩放2倍即可。 可以发现，当A位于这个圆的内部的时候，△ABC也不存在Malfatti正方形的构造。

5、 继续参考《Malfatti测试3》。 再构造△A''BC，使得△A''BC与△BCA相似，那么A''的轨迹是一条直线，当A跑到直线左边的时候，不存在Malfatti正方形的构造。

6、 继续参考《Malfatti测试3》。 现在有三个“禁区”——两个圆和一条直线，作它们关于点U的对称图形，就得到了六个“禁区”。 只要A不跑到两条直线所夹区域之外、四个红色圆内部，就一定存在满足要求的三个正方形。 完整的课件，请参考官网《Malfatti正方形中级版》。（之所以叫中级版，因为我的图中的A“不敢跑到”直线下面去，否则乱套！）