【平面几何】细致理解Desargues对合定理

关于Desargues对合定理，在百度百鹊蓄库味科里面有明确介绍：通过一个已知四点形的顶点所作的二次曲线束与不通过任何一个顶点的直线相交成一对合，其中以同一条二次曲线与该直缏堋垌胯线的交点为对合对应点。百度百科给出的证明方法，属于代数方法，严禁却不够直观。本文，将用一种简单而直观的方法来解释这个定理，只不过这个方法不够严谨。

工具/原料

电脑

网络画板

先画图

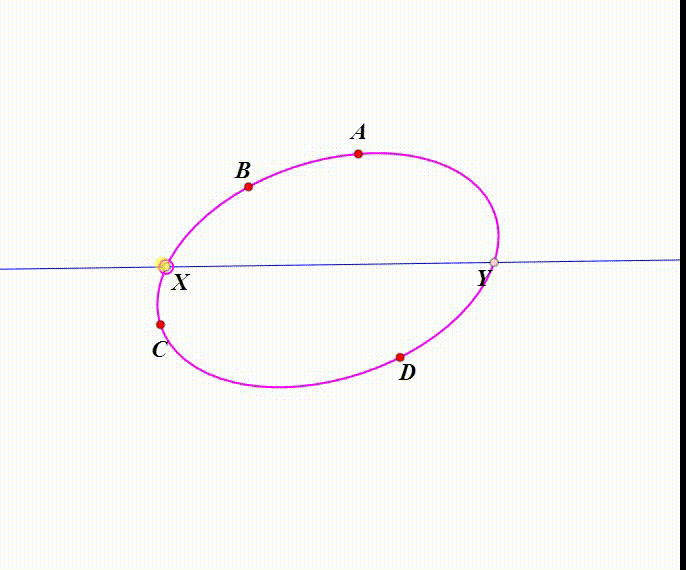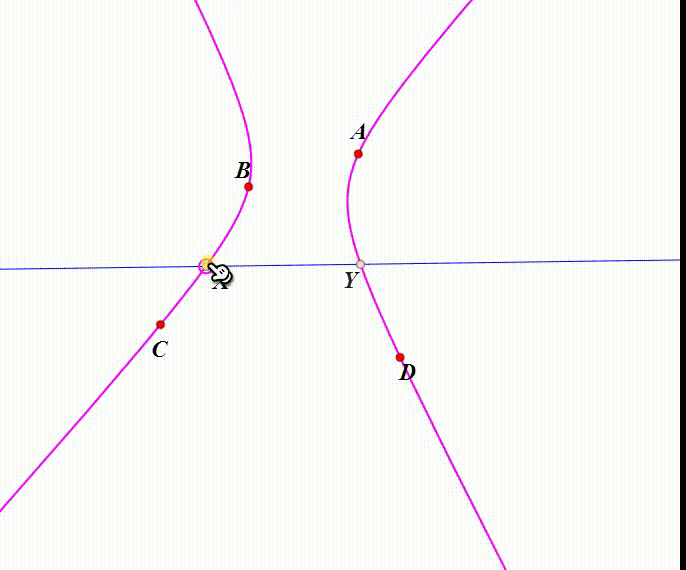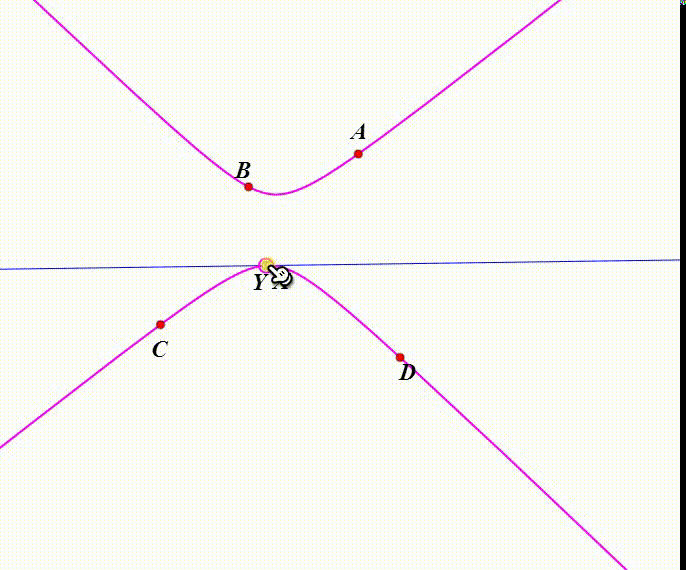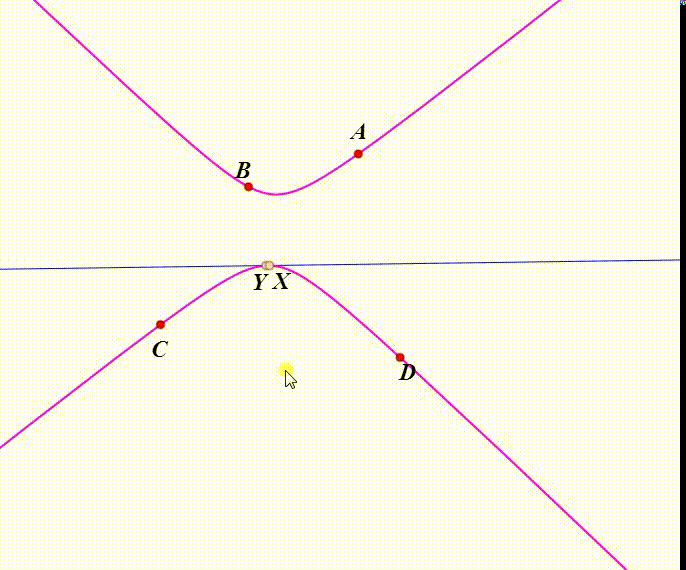
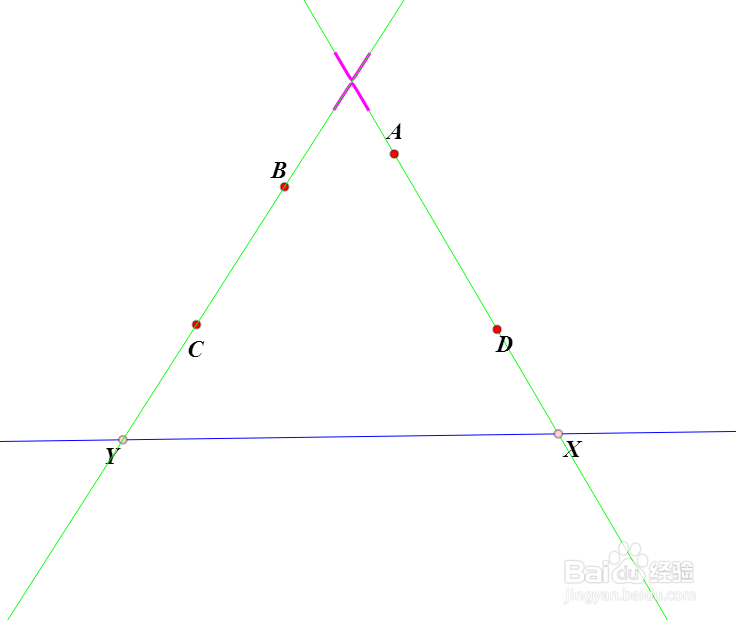
1、先来画出需要的图像：给定定理中四点形的四个顶点A、B、C、D，要求任意三点不共线。

2、画一条直线EF，要求EF不经过A、B、C、D任意一点。

3、在直线EF上选一个动点X。

4、选中A、B、C、D、X五个点，构造【过五点圆锥曲线】，设这条曲线为Ω。

5、设Ω与直线EF的另一个交点是Y。

6、X是动点，那么X和Y是对合。

7、当X和Y重合，所在位置就是对合的不动点，或者说叫做二重元素。当直线EF处于不同位置的时候，不动点的数目可能不相同。

8、当A、D、X共线，那么B、C、Y共线；此时，二次曲线Ω退化为双直线AD和BC。

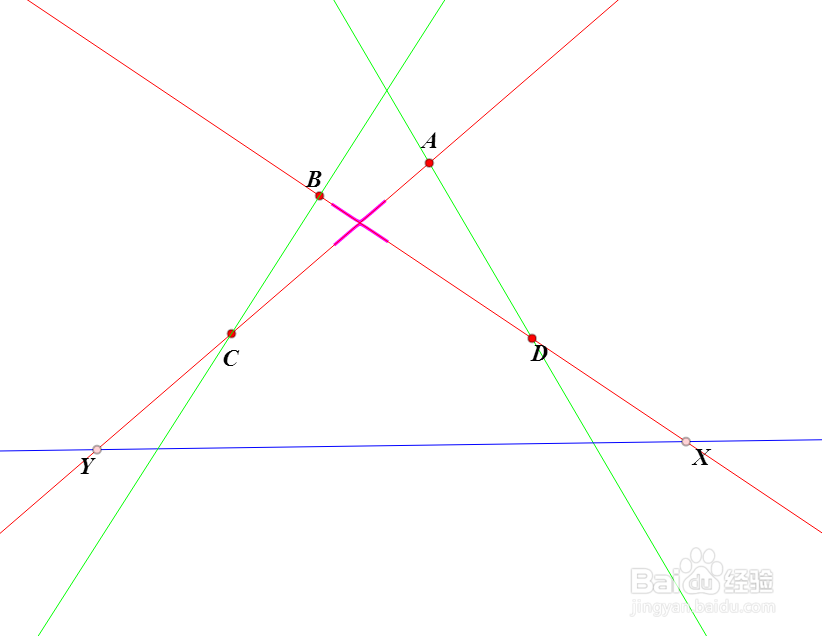
9、当B、D、X共线，那么A、C、Y共线。此时，AD、BC、BD、AC围成一个完全四边形。

直观理解

1、先介绍两个事实：事实之一——————平面上任意三点不共线的五点确定一条圆锥曲线。特殊情况是，如果其中某三点共线，另外两点就确定另一条直线，这就是双直线。

2、事实之二——————平面上直线EF与二次曲线Ω（上面四点A、B、C、D和X确定的二次曲线犬匮渝扮）只有两个交点。需要注意的事情是：1、如果二次曲线Ω与直线EF相切，可以视为两个交点重合；2、如果二次曲线Ω与直线EF不相交（比如椭圆与直线EF相离），可以视为二者有两个虚交点；3、如果二次曲线Ω退化为双直线（任意三点不共线的四个点A、B、C、D决定了二次曲线Ω不可能退化为单直线的平方），而直线EF不经过A、B、C、D任意一点，那么直线EF与双直线Ω有两个交点。4、特别的，如果EF与双直线Ω的某一分支平行，则其中一个交点就是无限远点。如下图，EF//BC，且A、D、X共线，那么Y就是BC与EF在无限远处的交点。

3、对合，可以理解为一个变换过程f：f(f(X))=X下面我就来说明这个变换Y=f(X)的具体过程：平面上给定四个顶点A、B、C、D，直线呶蓟鹭毵EF不经过A、B、C、D四点，X是EF上的任意一点，A、B、C、D、X五点确定一条二次曲线Ω，直线EF与Ω相交于异于X的点Y，就是f(X)=Y的具体过程。这个过程也有f(Y)=X，因此这是一个对合，不需要代数证明。