用FixedPointList来绘制分形图形

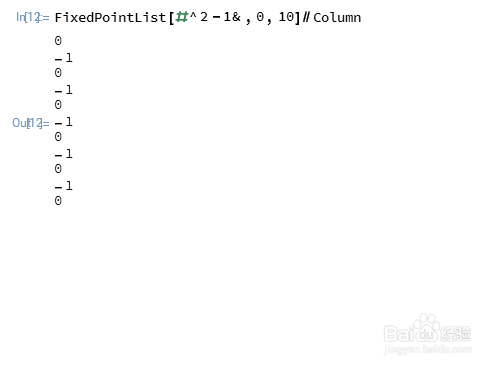
1、FixedPointList的作用，是求出一个迭代的不动点，并且返回每一步迭代的结果:FixedPointList[#^t+c&,0,10]这个代码的作用是，进行以下迭代：z=z^2+c，z的初始值是0，迭代10次。由于c是未知数，所以这个迭代是没有不动点的。

2、如果，令t=2，把c代入具体的复数，看看迭代效果。当c=-1，数值在0和-1之间波动，没有不动点。当c=1的时候，迭代过程是发散的。

3、可是，实验了几个数值，这个迭代是否发散，还是没有找到规律。不过，我们知道有一个结论，如果某一个复数c的模长大于2，这个迭代是一定会发散的。所以在迭代过程中，如果某一步的结果的模长大于2，就可以停止迭代了。FixedPointList[#^2-1-I&,0,20,SameTest->(Abs[#]>2&)]

4、用Length来看看，迭代多少次，结果会超过2。FixedPointList[#^2+-1-I/3&,0,20,SameTest->(Abs[#]>2&)]//Length从运行结果可以看出来，当c=-1+I/3的时候，第13次迭代的结果的模长大于2。

5、如果把这个迭代作用于复平面上的某些点，看看不同的复数点着色，着色依据是以模长大于2的最少的迭代次数作为迭代参数。如下，对矩形区域-2-1.5 I到2+1.5 I之间的某些数字进行迭代，酴兑镗笄查看迭代次数。Table[Length[FixedPointList[#^2+x+I y&,0,20, SameTest->(Abs[#]>2&)]],{y,-1.5,1.5,0.5},{x,-2,2,0.5}]

6、用ArrayPlot把上面的数据转化为像素图，模长大于2的最少的迭代次数越小，这个点的颜色越浅。ArrayPlot[皈其拄攥Table[Length[FixedPointList[#^2+x+I y&,0,20, SameTest->(Abs[#]>2&)]],{y,-1.5,1.5,0.5},{x,-2,2,0.5}]]

7、用彩色图来代替黑白图。ColorFunction->"Rainbow"这个的染色的深浅，我真的不懂了。不过，迭代的次数不同，颜色就不同，这点是不会错的。

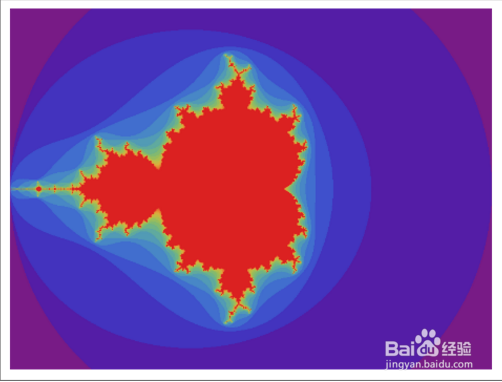
8、把图像细化一下，像素细化为原来的10倍，看起来有了Mandelbrot分形的雏形了：{y,-1.5,1.5,0.05},{x,-2,2,0.05}

9、再细化一下，细化为100倍：{y,-1.5,1.5,0.005},{x,-2,2,0.005}这个已经很好了。