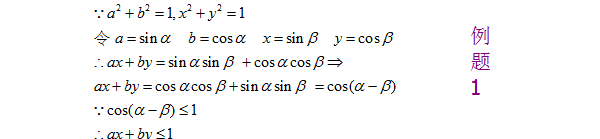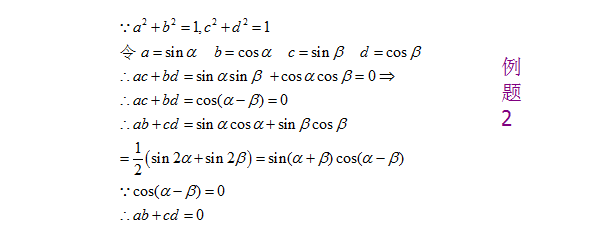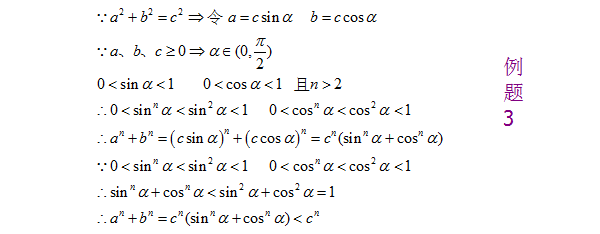如何使用三角代换求解代数问题

1、例题1：已知：a^2+b^2=1，x^2+y^2=1，求证ax+by≤1。分析：这里可以巧用“1”的关系，即(cost)^2+(sint)^2=1这一关系，所以我们可以使用三角代换，求解此题，具体解答过程如下图所示：

2、例题2：已知：a^2+b^2=1，c^2+d^2=1，并且ac+bd=0，求ab+cd的值。分析：这里同样可以巧用“1”的关系，所以我们可以使用三角代换求解此题，具体解答过程如下图所示：

3、例题3：已知：a^2+b^2=c^2，a、b、c都是正数，求证a^n+b^n<c^n。分析：这里要变换一下如何巧用“1”的关系，即把三角代换变化为三角函数的c倍，所以我们可以使用三角代换，求解此题，具体解答过程如下图所示：

4、例题4：已知：方程为：x+x/(√(x^2-1)=2√2，求此方程的解。分析：此处有(x^2-1)的关系，联想到(secβ)^2-1=(tanβ)^2,具体求解过程如下图所示：

5、例题5：已知：/a/<1，/b/<1，求证/(a+b)/(1+ab)/<1。分析：此题利用三角函数的值域，因为正余弦函数值的绝对值小于等于1，所以此题我们依然使用三角代换求解，具体求解过程如下图所示：