算面积平方怎么算

本文，用Mathematica来计算各种平面图形的面积。

工具/原料

电脑

Mathematica

三角形的面积

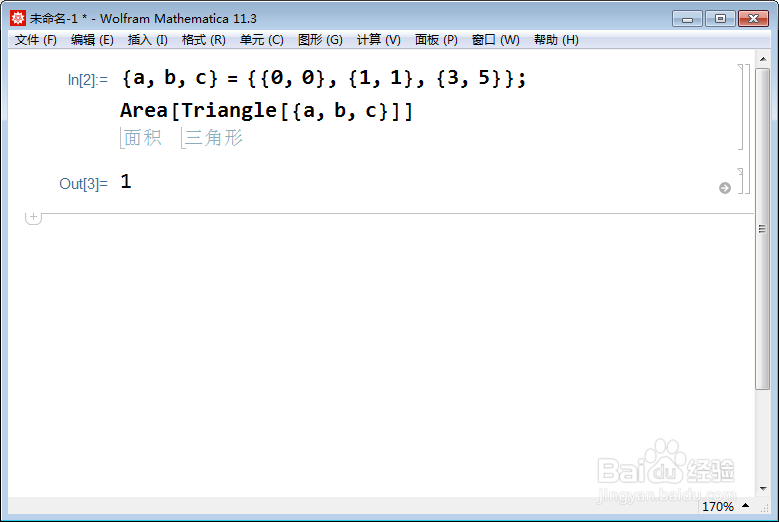
1、三角形是平面单形，如果知道了三个顶点的坐标，就可以算出面积。方法有多种：{a, b, c} = {{0, 0}, {1, 1}, {3, 5}};Area[Triangle[{a, b, c}]]，这算出的就是三角形abc的面积，三个顶点坐标用a、b、c表示。

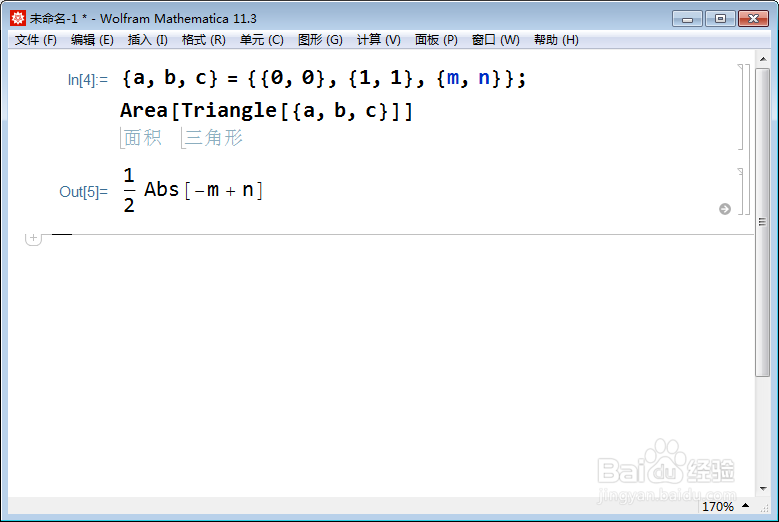
2、如果坐标中出现未知变量，那么面积公式中，就会出现绝对值符号。{a, b, c} = {{0, 0}, {1, 1}, {m, n}};Area[Triangle[{a, b, c}]]。这其实是绝对面积，或称为有向面积的绝对值。

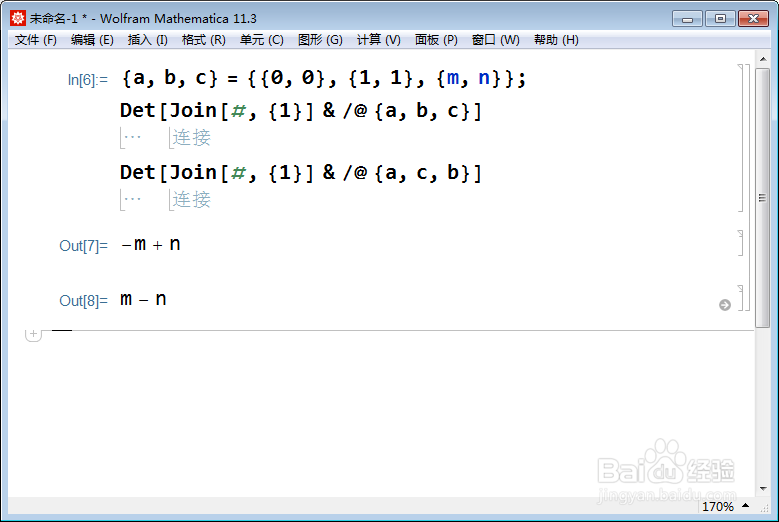
3、如果要计算有向面积，那就与三个顶点的字母顺序有关系了。{a, b, c} = {{0, 0}, {1, 1}, {m, n}};Det[Join[#, {1}] & /@ {a, 芟鲠阻缒b, c}]——一个方向的面积；Det[Join[#, {1}] & /@ {a, c, b}]——另一个方向的面积。平面上的三角形的有向面积有两个方向，大小相等，符号相反。还差一个系数。

多边形的面积

1、以下面四点为坐标的四边形：A = {{0, 0}, {1, 1}, {1, 2}, {2, 3}};作出图像来看看：Graphics[{Blue, Polygon[A]}]。

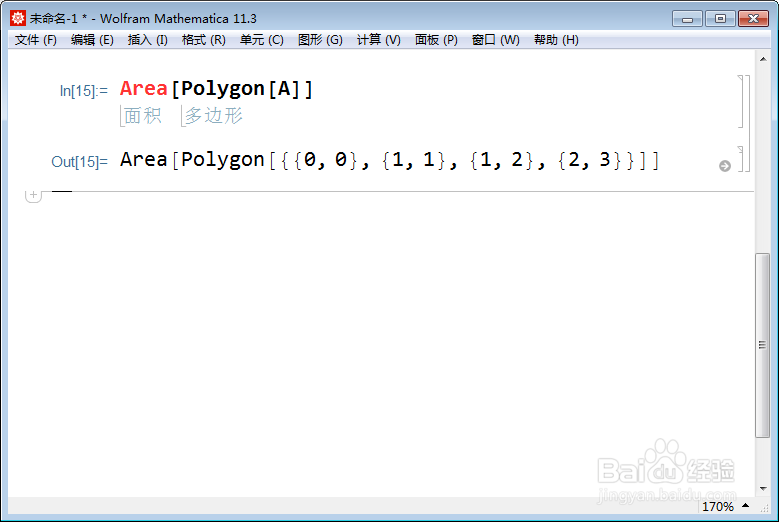
2、直接算面积，是行不通的。Area[Polygon[A]]。

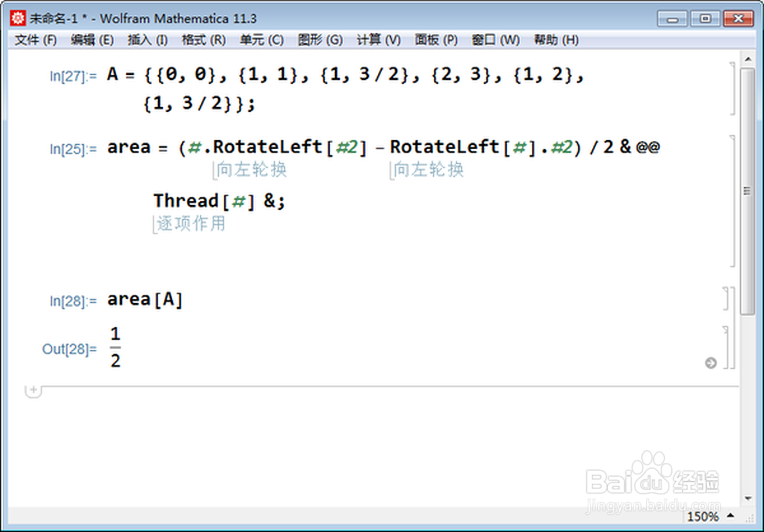
3、剩下的办法，就是求出交叉四边形的交点坐标，来计算绝对面积。面积是1/2。下面是函数：area = (#.RotateLeft[#2] 幻腾寂埒- RotateLeft[#].#2)/2 & @@ Thread[#] &;交点坐标是Q={1,3/2}，多边形的面积是：Abs[area[ {{0, 0}, {1, 1}, Q, {2, 3}, {1, 2}, Q}]]