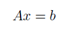线性代数问题，求矩阵的对角阵时为什么要把特征向量单位化呢

因为P是正交矩阵，正交矩阵每一行（或列）都是单位向量，题中A恰有3个不同的特征值，而不同特征值对应特征向量必正交，所以就不用正交化，而是直接疟觥窖捎单位化。

一般情况下，若λ0是A的特征值，且是特征多项式的k重根，因为A可对角化，所以特征方程│A-λ0│=0的基础解系必包含k个解向量，则这k这个特征向量必须施密特正交化然后再单位化。

有定理：矩阵A可对角化的充分必要条件是A的每个特征值的代数重数等于其几何重数，即A有完全特征向量系。

一、线性代数的介绍

“线性代数”是理工科大学生必修的数学基础课之一，也是硕士研究生入学全国统一考试中必考的数学课程之一。

通过线性代数课程的学习，不仅可以掌握该课程的基础理论，更重要的是可以培养学生的空间直观和想象能力以及抽象思维和逻辑推理能力、为学习后续课程和进一步扩大实践能力打下必要的数学基础。

二、线性代数基本概念和符号

线性代数可以对一组线性方程进行简洁地表示和运算。例如，对于这个方程组:

这里有两个方程和两个变量，如果你学过高中代数的话，你肯定知道，可以为x1 和x2找到一组唯一的解 (除非方程可以进一步简化，例如，如果第二个方程只是第一个方程的倍数形式。但是显然上面的例子不可简化，是有唯一解的)。在矩阵表达中，我们可以简洁的写作:

其中：