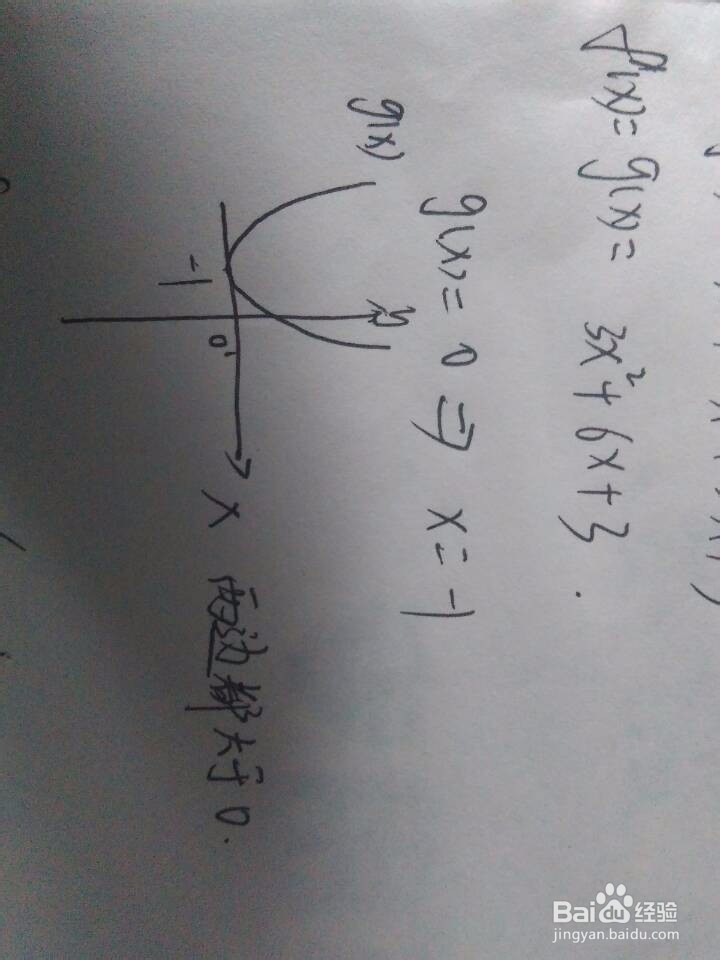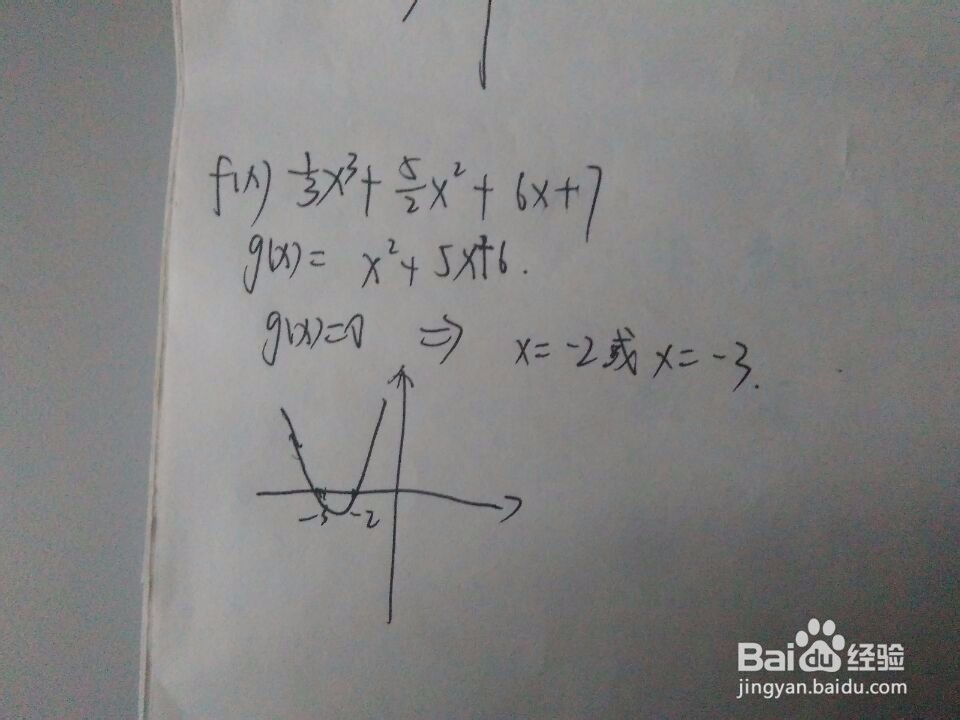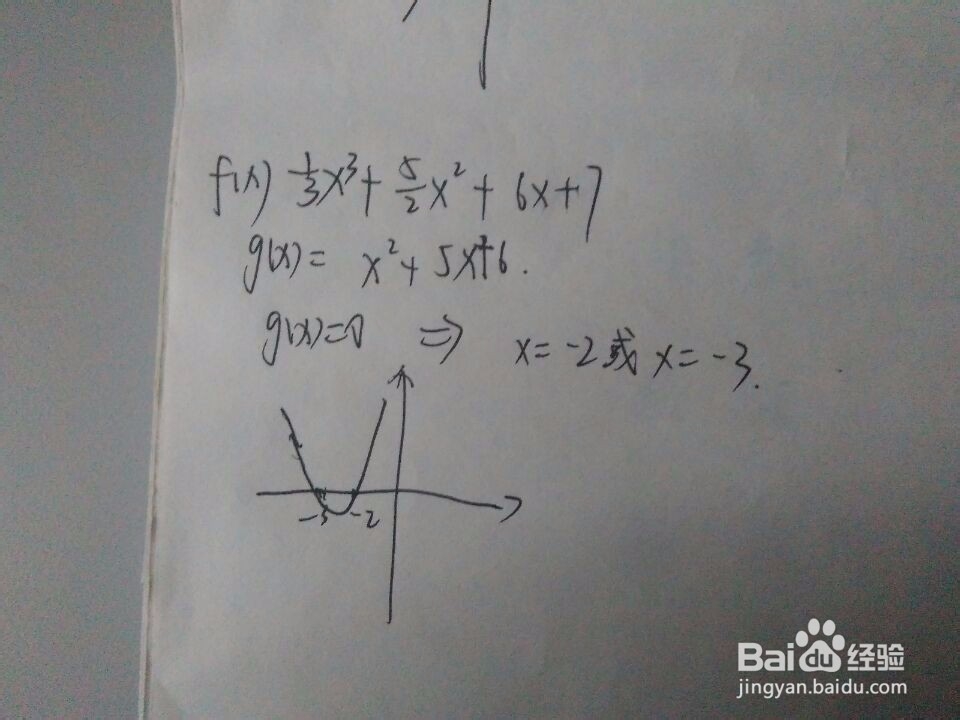如何求复杂函数的最值

1、先求其导函数。比如，f(x)=x^3+3x^2+3x+3,用导函数的方法求就是：（设g（x)是fx的导函数，gx=3x^2+6x+3;

2、令导函数等于0，求解对应的方程。令gx=0，可得x=-1;

3、根据导函数的函数图像特征来判断该点是极大值点还是极小值点，或者是既不是极大值点也不是噍祧鲚歇极小值点。根据g旌忭檀挢x的图像特征可知，在x=1这一点的左边gx是大于0的，右边gx也是大于0的，根据“导函数大于0，函数是递增的”这一性质，可知fx在定义域内递增，因此fx没有极值点，于是更没有最值点。

4、再举一个例子。写到这个步骤时，突然发现这个函数缺少一般性，不能向读者展示求复杂函数的一般方法。再举一个挣窝酵聒函数吧，fx=(1/3)*(x^3)+(5/2)*(x^2)+6x+7,（定义域是【-7，-1】）这个函数，其导数是x^2+5x+6,令该导数等于0，即求x^2+5x+6=0这个方程，解得x=-2或x=-3；

5、然后画出x^2+5x+6这个函数的图像。可以发现，在x=-2的右侧，还有x=-3的左侧，导函数都是大于0的，而在-2和-3之间，导函数是小于0的。根据性质有，fx在x<-3或x>-2时是递增的，而在-3和-2之间是递减的。

6、根据函数图像可知-3是极大值点，-2是极小值点。

7、再来看看定义域，是【-7，-1】，两边都是闭的，于是将两端的值和极大极小值进行比较，即分别求得f(-7),f(-1),f(-3),f(-2)的值，进行比较，最小的那一个即为最小值，最大的那一个就是最大值。