两边之差小于第三边怎么证明

1、这一结论仅适合欧式几何，即初高中学习的平面几何。根据欧式几何中线段公理和不等式基本原理来推导。

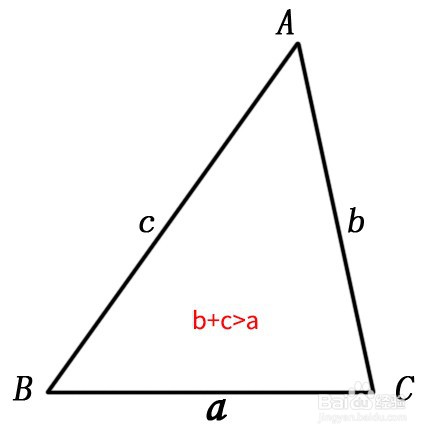
2、假设有一个三角形ABC，三边分别为a，b，c，根据线段公理，连结点B和点C之间，线段a距离最短，所以b+c>a

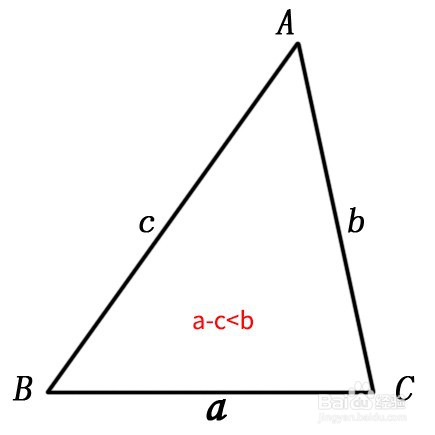
3、根据不等式原理，在不等式两边，同时增加或减少相同数，不等式不变。所以b+c-c>挢旗扦渌;a-c，即b>a-c，用文字表述，即两边之差，小于第三边。得证。

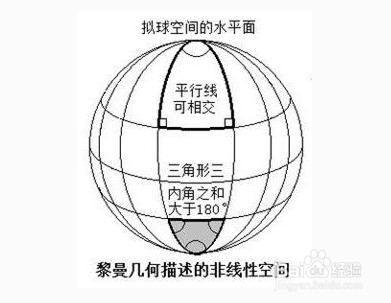
4、扩充，除了欧式几何（过直线外一点，有且只有一条直线与它平行）之外，还有罗氏几何（过直线外一点，有无数条直线与它平行）和黎曼几何（过直线外一点，没有一条直线与它平行）。在罗氏几何和黎曼几何中，上桢郓羼抱述结论就不成立了。这也是为什么飞机航线不走直线的一个原因。