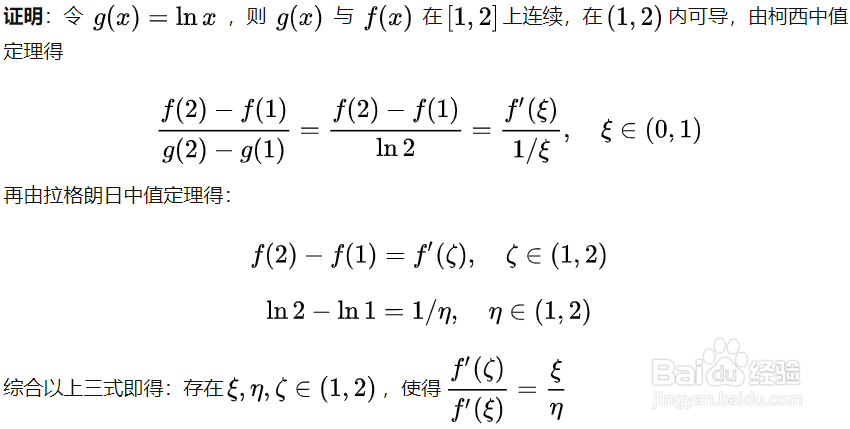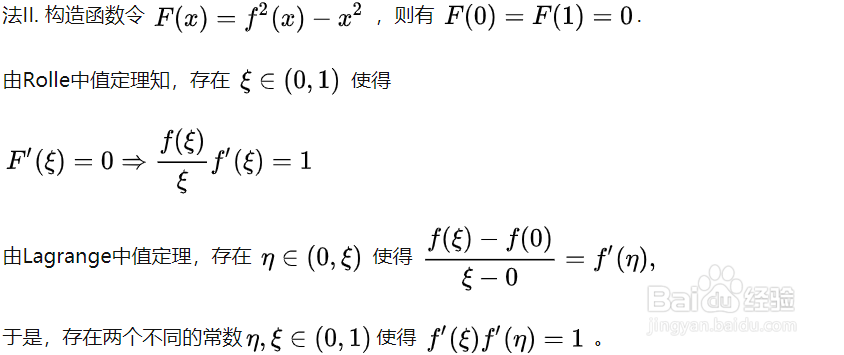多次中值定理题目的解题思路

很多题目需要多次运用中值定理，本文对这一类的题目具体用哪一个中值定理进行总结分析。

本文的结论

1、(1) 拉格朗日中值定理与柯西中值定理可以互相建立联系(可以抵消).(2) 从形式上看：拉格朗日中值定理是 1 个；柯锚翦迩撸西中值定理是 2 个. 那么ξ的个数为 1 个，则用拉格朗日；ξ的个数为 2 个(乘除)，则用柯西.若要求ξ^n互不相等，则需要分段。分段方式大致有两种：➀分段点可以抵消(需要构造分段点的值)；➁分段点为ξ^n，则很可能是利用Cauchy中值定理反复求导来套娃(3) 一把牛刀：Darboux定理

第一类：不要求ξ^n互不相等

第二类：要求ξ^n互不相等

Darboux定理的应用