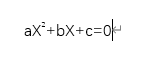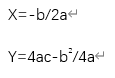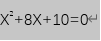二元函数求极值的步骤

1、拿到一个二次函数，不要着急算，先分析，先看拿到的二次函数是否是，一般式，不是一般式的先换成一般式。一般建议将二次函数的二次项系数换成1，但是也有例外，下面也会讲，我们先用这个基本式子进行讲解

2、第一步先确定开口方向

3、我们都知道二次函数的图像是一个抛物线，二次函数求极值（最大值，最小值），首先我们先来说最简单的，定义域没有限制，在整个抛物线中，如果开口向上，则二次函数只有最小值没有最大值。我们在回答时只需要回答最小值是多少？没有最大值就可以反之，如果开口向下二次函数只有最大值，没有最小值。

4、在确定完开口方向以后，我们可以根据公式求二次函数的对称轴，根据对称轴x所在的位置，我们可以在二次函数镖镐守悉抛物线上，找到对应一点y的值，此处也是顶点坐另外，我们可以将所求的对称轴x值代入到二次函数中，求出所对应的y，这两种所求的值都是一样的，我们也可以作为一种验证。

5、这样根据开口方向我们就可以确定二次函数的极值是最大值还是最小值了。

6、刚才我们所讲解的求二次函数求极值都是最简单最基础的，我们可以发现在考试或是做题中很多的，X的定义域都是有要求的，所以下面我们就来仔细的讲解一下在x的定义域内该如何求二次函数的极值。下面我们的讲解就用一个具体的二次函数来说,以便更好地理解。

7、第一步我们看二次函数是否是一般式，第二步确定开口方向，第三步，求对称轴x所对应的位置，求出定点坐标。

8、现在我们已经将二次函数处理好了。接下来我们将二次函数X给定义域。基础步骤还是与上面相同，只是需要确定对称轴是否在区间内，根据这个定义域我们可以发现，二次函数在这个区间内是递增的，洹彭岣啬而且这个区间是一个闭区间，所以二次函数的极值我们可以轻松求出来。

9、下面我们换一个x的定义域，基础步骤还是与上面相同，只是需要确定对称轴是否在区间内，可以看到，对称轴是在区间内的，所以这个时候的极值就需要计算比对一下了，我们需计算区间头的值和顶点的值。

10、将三点的y值进行比对，可以知道最大值与最小值

11、另外定义域还有各种各样的变化，只需要根据题意去分析即可，但是过程都不变，也可以自己总结一下，只需要按照规则取计算就可以了，我们求极值一般都是数图结合的，这也是最好用的办法，以后还会接触到各种各样求极值的题，可以通过图形结合找突破口。