如何设计正交试验

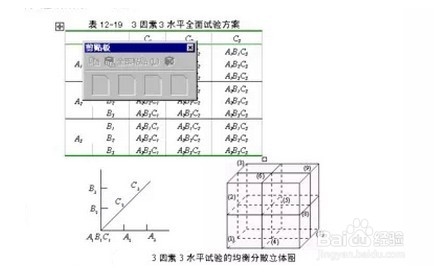
1、基本简介：当分析因设计要求的实验次数太多时，一个非常自然的想法就是从析因设计的水平组合中，选择一部分有代表性水平组合进行试验。因此就出现了分式析因设计(fractional factorial designs)。正交设计的基本特点是：用部分试验来代替全面试验，通过对部分试验结果的分析，了解全面试验的情况。正交试验是用部分试验来代替全面试验，它不可能像全面试验那样对各因素效应、交互作用一一分析；当交互作用存在时，有可能出现交互作用的混杂。

2、正交表：正交表是一整套规则的设计表格。用L为正交表的代号，n为试验的次数，t为水平数，c为列数，也就是可能安排最多的因素个数。例如L9(34)，它表示需作9次实验，最多可观察4个因素，每个因素均为3水平。一个正交表中也可以各列的水平数不相等，称它为混合型正交表，如L8(4×24) ，此表的5列中，有1列为4水平，4列为2水平。根据正交表的数据结构看出，正交表是一个t行c列的表，其中第j列由数码1，2，… Sj 组成，这些数码均各出现N/S 次。

3、正交表具有两条性质：(1)每一列中各数字出现的次数都一样多。(2)任何两列所构成的各有序数对出现的次数都一样多。所以称之谓正交表。

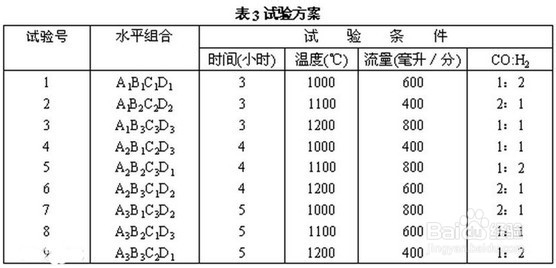
4、方案设计：安排试验时，只要把所考察的每一个因子任意地对应于正交表的一列(一个因子对应一列，不能让两个因子对应同一列)，然后把每列的数字"翻译"成所对应因子的水平。这样，每一行的各水平组合就构成了一个试验条件(不考虑没安排因子的列)。例：某矿物气体还原试验中，要考虑还原时间(A)、还原温度(B)、气体流速(C)、还原气体比例(D)这四个因子对全铁合量X〔越高越好)、金属化率Y(越高越好)、二氧化钛含量Z(越低越好)这三项指标的影响。希望通过试验找出主要影响因素，确定最适工艺条件。　　首先根据专业知以确定各因子的水平：　　时间：A1=3(小时)，A2=4(小时)，A3=5(小时)　　温度：B1=1000(℃)，B2=1100(℃)，B3=1200(℃)　　流速：Cl=600(毫升/分)，C2=400(毫升/分)，　　 C3=800(毫升/分)　　 CO:H2：D1=1:2，D2=2:1，D3=1:1　　这是四因子3水平的多指标(X、Y、Z)问题，如果做全面试验需3^4=81次试验，而用L9( 34)来做只要9次。具体安排如表3。

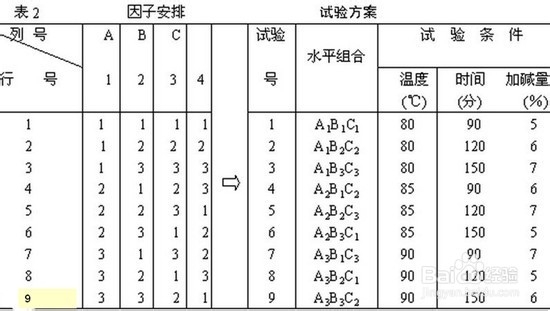
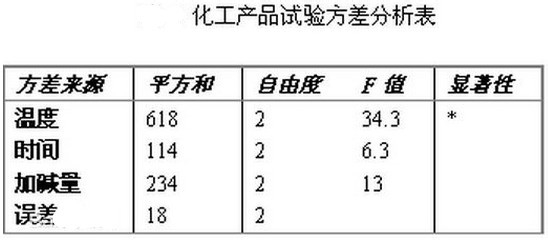
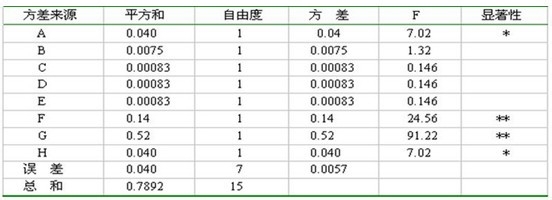
5、数据分析—方差分析：正交表的另一个好处是简化了试验数据的计算分折。还是以[例1]为例来说明。按照表2的试验方案进行试验，测得9个转化率数据。由总平方和与各因素平方和即可求得误差平方和，亦称剩余平方和。是总平方和减各因素平方和所得。如正交表有一空列，则该列的平方和就是误差平方和。但在正交表饱和试验的情况下，即所有各列全部排满时，误差平方和一般用各因素平方和中几个最小的平方和之和来代替，同时，这几个因素不再作进一步的分析。　　自由度：φT=试验次数一1　　φA,B…=水平数一1　　φA×B=φA×φB　　φe=φT-φA-φB-……-φD