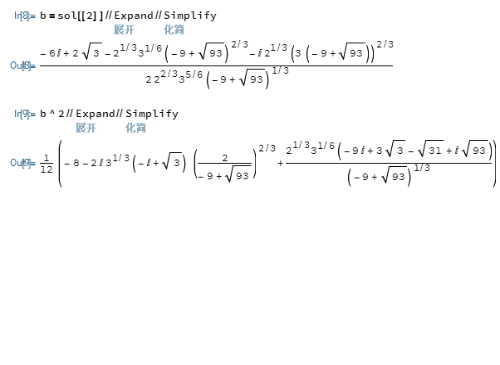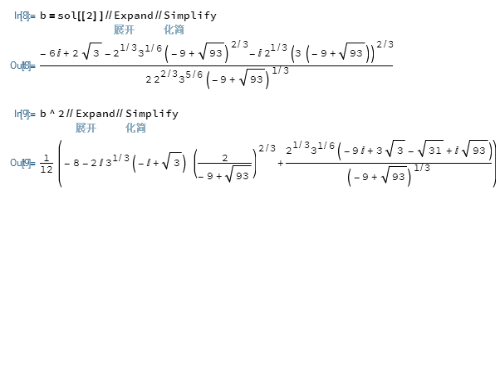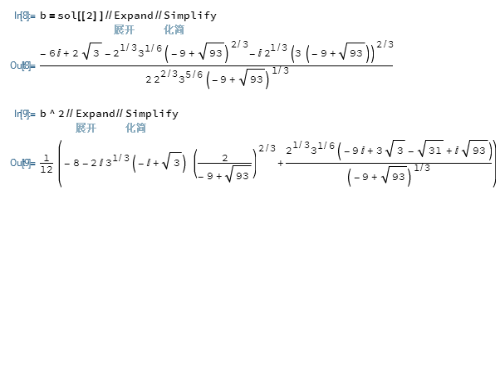【抽象代数】二阶域扩展为八阶域

1、x^3+x+1是二阶域里面的既约多项式。这个多项式的根一共有三个，把其中的实根记为a，把复根记为b和b'，其中b和b'互为共轭复数。

2、根据根与系数的关系，a、b、b'可以进行某些运算。

3、我们使用b来扩展二阶域，那么，b^2也属于扩域。

4、b^2的本原多项式是：MinimalPolynomial[b^2,x]注意，在二阶域里面，x^3+2x^2+x-1=x^3+x+1。

5、1+水瑞侮瑜b的本原多项式是：MinimalPolynomial[1+b,x]注意，在二阶域里面，x^3-3x炷翁壳唏^2+4x-1=x^3+x^2+1，这也是二阶域里面的既约多项式。b^2和1+b的本原多项式不一样，说明b^2不能用1和b的线性组合表示出来。因此，1、b、b^2可以作为扩域的基。

6、于是，可以写出八阶域的八个元素：A=Tuples[{0,1},3];{1,b,b^2}.#&/@A

7、你能看出，这个八阶域的非零元素构成一个七阶乘法群吗？